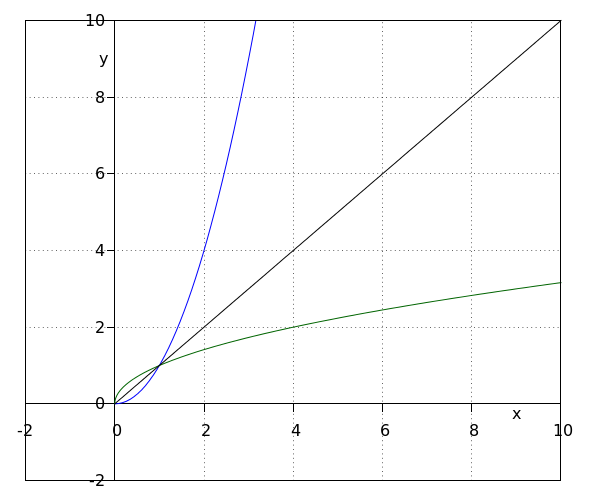
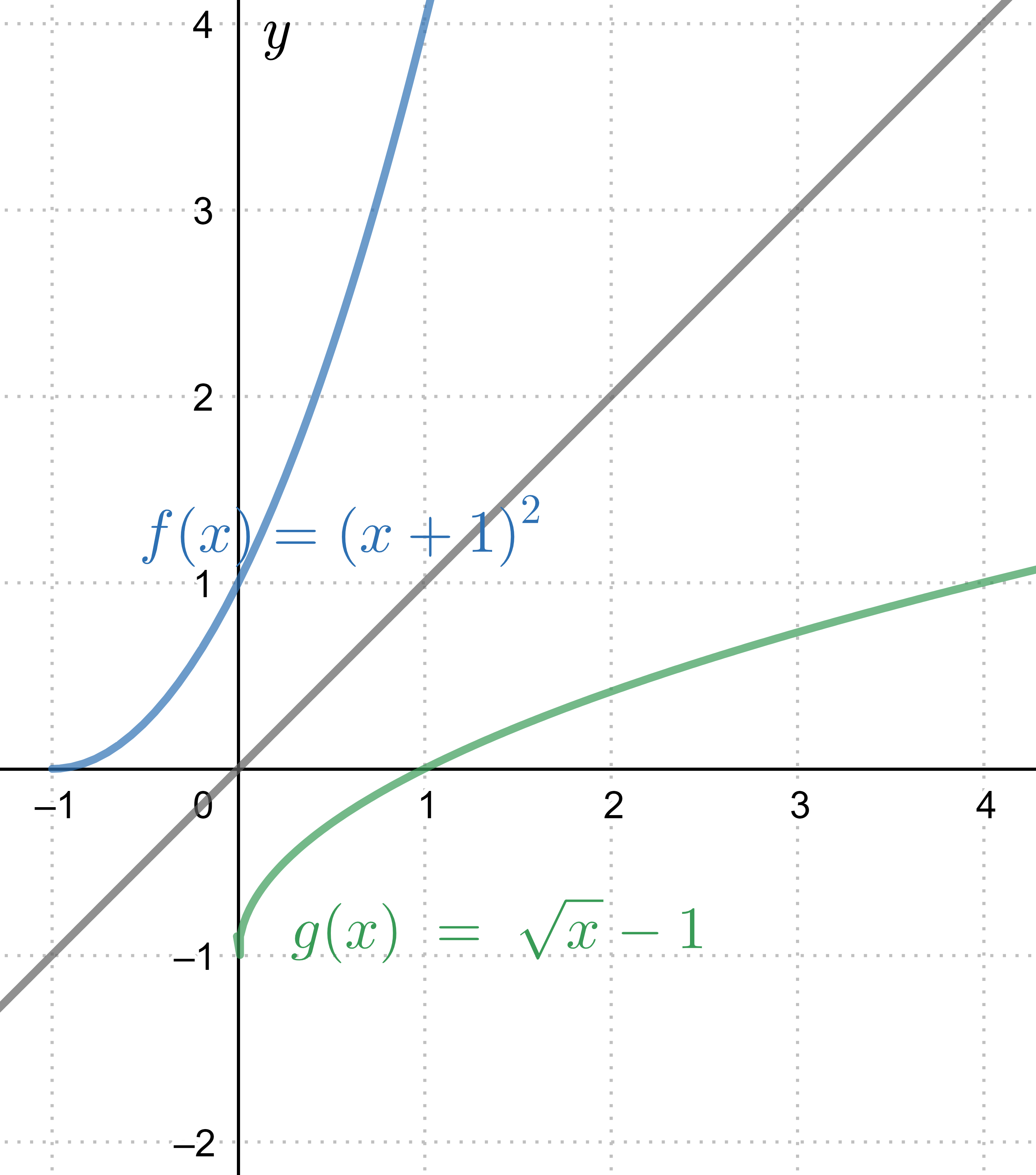Echamos un vistazo a las funciones #\blue{f(x)}=\blue{x^2}# y #\green{g(x)}=\green{\sqrt{x}}# en el dominio #\ivco{0}{\infty}#.
Para estas funciones, tenemos #\blue f(\green{g(x)})=\left(\green{\sqrt{x}}\right)^\blue2=x# para toda #x# en #\ivco{0}{\infty}#.
Por lo tanto, #\green{g(x)}# se denomina inversa de #\blue{f(x)}#.
También tenemos #\green g(\blue{f(x)})=\green{\sqrt{\blue{x^2}}}=x# para toda #x# en #\ivco{0}{\infty}#.
Por lo tanto, #\blue{f(x)}# se denomina inversa de #\green{g(x)}#.
La función #\blue{f(x)}# tiene una función inversa #\green{g(x)}# si \[\blue f(\green{g(x)})=x\]
Desde una perspectiva geométrica, la gráfica de la inversa de #\green{g(x)}# es la reflexión de #\blue{f(x)}# sobre la línea #y=x#.
También podemos anotar el inverso de #f(x)# por #f^{-1}(x)#.
Al determinar la función inversa de una función, el dominio de esa función es importante. El dominio de #\blue{f(x)}# es el rango de #\green{g(x)}# y el dominio de #\green{g(x)}# es el rango de #\blue{f(x)}#. Por tanto, la función inversa #\green{g(x)}# se define en el rango de función #\blue{f(x)}#.
Ejemplo
En la gráfica #\blue{f(x)}=\blue{(x+1)^2}# en el dominio #x \ge -1# y su inversa #\green{g(x)}=\green{\sqrt{x}-1}# en el dominio #x \ge 0#
El dominio de la función #\blue{f(x)}=\blue{(x+1)^2}# consta de todos los números y su rango consta de todos los números no negativos. Así, su función inversa #\green{g(x)}=\green{\sqrt{x}-1}# tiene como dominio solo los números no negativos, donde su rango es también solo los números no negativos. Por lo tanto, la función #\blue{f(x)}=\blue{(x+1)^2}# solo tiene una inversa en el dominio de todos los números no negativos.
Al revés, tenemos que la función #\green{g(x)}=\green{\sqrt{x}-1}# tiene la función #\blue{f(x)}=\blue{(x+1)^2}# como inversa, pero solo en el domino de todos los números mayores o iguales que #-1#. Porque ese es el rango de #\green{g(x)}# y así el dominio de #\blue{f(x)}#.
En general, no mencionamos estas limitaciones en el dominio de la función inversa, pero las asumiremos implícitamente.
| | Procedimiento Determinamos la función inversa #\green{f^{-1}(x)}# de la función #\blue{f(x)}#. | Ejemplo #\blue{f(x)}=\left(x-4\right)^2#. |
| Paso 1 | Escribe la función como una fórmula, por lo tanto, en la forma #y=\ldots#.
| #y=\left(x-4\right)^2# |
| Paso 2 | Aísla la variable #x# en la fórmula #y=\ldots#. Esto significa que la fórmula se escribe como #x=\ldots#.
| #x=\sqrt{y}+4# |
| Paso 3 | En la fórmula, cambia el #y# en #x# y #x# en #y#.
| #y=\sqrt{x}+4# |
| Paso 4 | Reemplaza #y# por #\green{f^{-1}(x)}#.
| #\green{f^{-1}(x)}=\sqrt{x}+4# |
Resolvemos el paso 2 a partir del ejemplo. Allí queremos aislar la variable #x# en la fórmula #y=\left(x-4\right)^2#. Esto se hace mediante reducción.
\[\begin{array}{rcl}y&=&\left(x-4\right)^2 \\ &&\phantom{xxx}\blue{\text{fórmula original}} \\ \sqrt{y}&=&x-4 \\ &&\phantom{xxx}\blue{\text{se extrajo la raíz de ambos lados }} \\ \sqrt{y}+4&=&x \\ &&\phantom{xxx}\blue{\text{ambos lados más }4}\end{array}\]
Por lo tanto, #x=\sqrt{y}+4#.
Ten en cuenta que aislar una variable en realidad es lo mismo que determinar la función inversa.
En ese caso, ya no tenemos que pasar por los pasos 3 y 4, y estamos listos en el paso 2 del procedimiento.
En el paso 2, tomamos la raíz cuadrada en ambos lados para poder aislar #x# fuera del cuadrado. Tomamos la raíz positiva. Como vimos en la introducción de la función de raíz la raíz de un número no negativo es un número no negativo.
Si se especifica cierto dominio para encontrar la inversa, podría ser necesario sacar la raíz negativa. En el ejemplo, #\blue{f(x)}# tiene un dominio de todos los números reales y un rango de todos los números no negativos. La función inversa #\green{f^{-1}(x)}# tiene como dominio todos los números no negativos y como rango, todos los números mayores o iguales que #4#. Por lo tanto, solo en el dominio #x \ge 4# la función #\blue{f(x)} = \blue{(x-4)^2}# tiene la inversa #\green{f^{-1}(x)} = \green{\sqrt{x}+4}#.
Si nos pidieran que calculáramos la inversa de #\blue{f(x)}# en el dominio #x\le 4#, deberíamos haber tomado la raíz negativa en el paso 2. La función inversa de#\blue{f(x)} =\blue{ (x-4)^2}# en el dominio #x \le 4# es #\green{f^{-1}(x) }= \green{-\sqrt{x}+4}#. Esta función tiene como dominio todos los números no negativos y como rango todos los números menores o iguales que #4#, que es exactamente el dominio dado.
Aísla #x# en
\[y=\sqrt{3\cdot x-2}\]
Da tu respuesta en la forma #x = ...#
#x={{y^2+2}\over{3}}#
#\begin{array}{rcl}
y&=&\sqrt{3\cdot x-2} \\ &&\phantom{xxx}\blue{\text{función original}}\\
y^2&=& 3\cdot x-2 \\ &&\phantom{xxx}\blue{\text{ambos lados al cuadrado}}\\
y^2+2&=&3\cdot x \\ &&\phantom{xxx}\blue{\text{ambos lados menos }-2}\\
{{y^2+2}\over{3}} &=&x \\ &&\phantom{xxx}\blue{\text{ambos divididos por }3}\\
x&=&{{y^2+2}\over{3}} \\ &&\phantom{xxx}\blue{\text{izquierdo y derecho intercambiados }}\\
\end{array}#
Funciones inversas
