Hoofdstuk 10: Variantieanalyse: Enkelvoudige variantieanalyse
 Enkelvoudige variantieanalyse: toetsingsgrootheid
Enkelvoudige variantieanalyse: toetsingsgrootheid
Zodra de hypothesen van een enkelvoudige variantieanalyse (enkelvoudige ANOVA) zijn geconstrueerd en willekeurige steekproeven zijn getrokken uit de verschillende populaties, is de volgende stap van de procedure de berekening van de toetsingsgrootheid die zal bepalen of de nulhypothese van gelijke populatiegemiddelden al dan niet verworpen wordt.
De berekening van de toetsingsgrootheid begint met het gebruiken van de steekproefgegevens om een schatting te krijgen van de populatiegemiddelden #\mu_i# en het algemeen populatiegemiddelde #\mu#.
Steekproefgemiddelde en algemeen steekproefgemiddelde
Laat #Y_{ij}# de gemeten waarde van de uitkomstvariabele zijn voor de #j#de waarneming in de steekproef die overeenkomt met niveau #i# van de factor.
Om een schatting te krijgen van de populatiegemiddelden #\mu_i#, berekenen we de steekproefgemiddelden #\bar{Y}_i#:
\[\bar{Y}_i = \cfrac{\displaystyle\sum^{n_i}_{j=1}Y_{ij}}{n_i}\]
Om een schatting te krijgen van het algemeen populatiegemiddelde #\mu#, berekenen we het algemene steekproefgemiddelde #\bar{Y}# :
\[\begin{array}{rcl}
\bar{Y} &=& \cfrac{\displaystyle\sum^I_{i=1}\displaystyle\sum^{n_i}_{j=1}Y_{ij}}{N} \\\\
&=& \cfrac{\displaystyle\sum^I_{i=1}n_i\bar{Y}_i}{N}
\end{array}\]
In een onderzoek naar de effecten van slaapgebrek op de rijvaardigheid werden #N = 15# deelnemers gerekruteerd en willekeurig toegewezen aan een van de #3# groepen: geen slaapgebrek (groep 1), 24 uur slaapgebrek (groep 2) of 48 uur slaapgebrek (groep 3).
Vervolgens werden de deelnemers in een simulator gezet en getest op verschillende rijvaardigheden, terwijl de onderzoekers het aantal gemaakte fouten bijhielden.
Hier is het aantal gemaakte fouten de uitkomstvariabele #Y# en is slaapgebrek de factor met #I=3# niveaus.
De hypothesen die worden getest zijn:
\[\begin{array}{rcl}
H_0&:& \mu_{0\,\text{uur}} = \mu_{24\,\text{uur}} = \mu_{48\,\text{uur}}\\
&&\text{(Alle populatiegemiddelden zijn gelijk, d.w.z., slaaptekort heeft geen effect op het aantal}\\
&&\text{gemaakte fouten.)}\\\\
H_a&:& \mu_{0\,\text{uur}} \neq \mu_{24\,\text{uur}} \,\text{ of }\, \mu_{0\,\text{uur}} \neq \mu_{48\,\text{uur}}\,\text{ of }\, \mu_{24\,\text{uur}} \neq \mu_{48\,\text{uur}}\\
&&\text{(Ten minste één populatiegemiddelde verschilt van een ander populatiegemiddelde,}\\
&&\text{d.w.z., slaaptekort heeft wel effect op het aantal gemaakte fouten.)}
\end{array}\]
De resultaten van het experiment zijn samengevat in de volgende tabel:
| Uren slaaptekort | ||||
| Groep 1 (0 uur) |
Groep 2 (24 uur) |
Groep 3 (48 uur) |
||
| 2 | 8 | 20 | ||
| 3 | 7 | 12 | ||
| 1 | 4 | 10 | ||
| 2 | 10 | 24 | ||
| 1 | 6 | 9 | ||
| Steekproefgemiddelde (#\bar{Y}_i)#: | 2 | 7 | 15 | Algemeen steekproefgemiddelde (#\bar{Y}#): 8 |
De berekeningen van de steekproefgemiddelden zijn:
\[\begin{array}{rcl}
\bar{Y}_i &=& \cfrac{\displaystyle\sum^{n_i}_{j=1}Y_{ij}}{n_i}\\\\
\bar{Y}_1 &=& \cfrac{2+5+0+2+1}{5}=2\\\\
\bar{Y}_2 &=& \cfrac{8+7+4+10+6}{5}=7\\\\
\bar{Y}_3&=& \cfrac{15+12+14+21+13}{5}=15\\\\
\end{array}\] En de berekening van het algemene steekproefgemiddelde is:
\[\begin{array}{rcl}
\bar{Y} &=& \cfrac{\displaystyle\sum^I_{i=1}n_i\bar{Y}_i}{N}\\\\
&=& \cfrac{(5\cdot2) + (5\cdot7) + (5\cdot15)}{15} = 8
\end{array}\]
Zodra de steekproefgemiddelden en het algemene steekproefgemiddelde bekend zijn, is de volgende stap het gebruik van deze gemiddelden om twee soorten varianties te berekenen: de variantie tussen steekproeven en de variantie binnen steekproeven.
Enkelvoudige ANOVA: toetstatistiek en nulverdeling
De variantie tussen steekproeven schat de verschillen tussen populaties en wordt berekend door het gemiddelde van elke steekproef te vergelijken met het algemene gemiddelde van de totale steekproef. 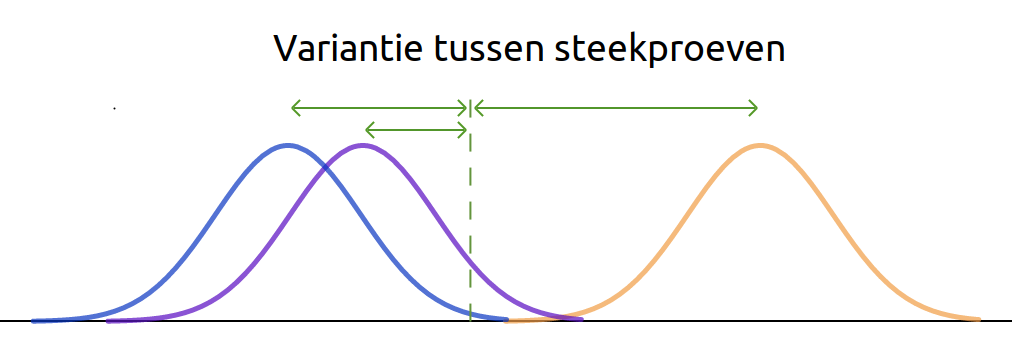
Variantie tussen steekproeven heeft twee mogelijke bronnen:
- Behandelingseffect. Er is sprake van een behandelingseffect als de nulhypothese onjuist is en ten minste één van de populatiegemiddelden verschilt van de andere. Als dit waar is, zouden we verwachten dat de steekproeven uit deze populaties ook verschillende gemiddelden zullen hebben.
- Stochastische fout. Zelfs als de nulhypothese waar is en alle populatiegemiddelden gelijk zijn, zouden we nog steeds verwachten dat er enkele verschillen tussen de steekproeven bestaan. Elke steekproef bestaat immers uit verschillende individuen, wat op zijn minst tot enige variatie tussen de steekproeven zou moeten leiden.
De variantie binnen steekproeven wordt berekend door de waarnemingen binnen elke steekproef te vergelijken met hun respectieve steekproefgemiddelde.
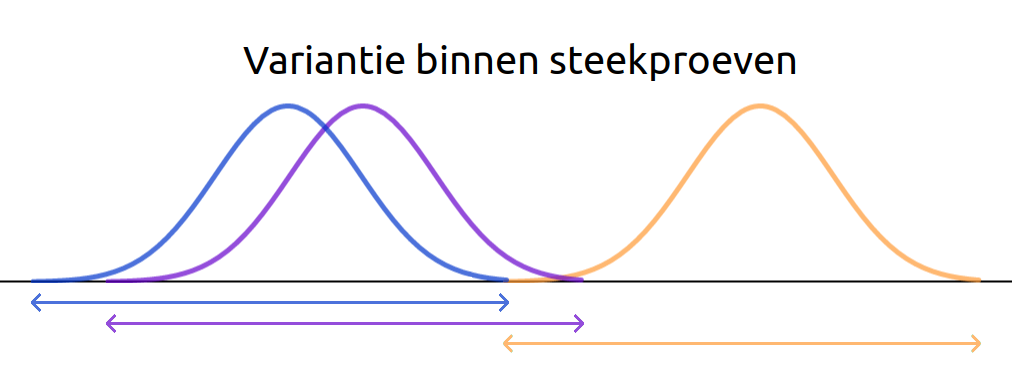
Omdat alle individuen binnen een steekproef uit dezelfde populatie komen, is de enige bron van variantie binnen steekproeven de stochastische fout.
De toetsingsgrootheid #F# van een enkelvoudige ANOVA wordt gedefinieerd als de verhouding tussen de variantie tussen steekproeven en de variantie binnen steekproeven:
\[F=\cfrac{\text{variantie tussen steekproeven}}{\text{variantie binnen steekproeven}}\] Als we de twee typen variantie uitdrukken in termen van hun mogelijke bronnen, wordt de definitie van de toetsingsgrootheid #F#:
\[F=\,\cfrac{\text{Behandelingseffect} + \text{Stochastische fout}}{\text{Stochastische fout}}\] Afhankelijk van of de nulhypothese waar is of niet, verwachten we verschillende waarden te zien voor deze toetsingsgrootheid #F#:
- Als de nulhypothese waar is en er geen behandelingseffect bestaat, dan zijn de gevonden verschillen tussen de steekproeven volledig toe te schrijven aan toeval. In dat geval meten zowel de variantie tussen steekproeven als de variantie binnen steekproeven alleen stochastische fouten en zouden we een toetsingsgrootheid #F# moeten vinden die ongeveer gelijk is aan #1#.
\[F=\,\cfrac{\text{Behandelingseffect} + \text{Stochastische fout}}{\text{Stochastische fout}}=\,\cfrac{0 + \text{Stochastische fout}}{\text{Stochastische fout}} \approx 1\] - Als daarentegen de nulhypothese onjuist is en er wel sprake is van een behandelingseffect, dan zou de variantie tussen steekproeven relatief groot moeten zijn in vergelijking met de variantie binnen steekproeven, en zouden we een toetsingsgrootheid #F# moeten vinden die aanzienlijk groter is dan #1#.
\[F=\,\cfrac{\text{Behandelingseffect} + \text{Stochastische fout}}{\text{Stochastische fout}}=\,\cfrac{\text{Behandelingseffect}}{\text{Stochastische fout}} + \,\cfrac{\text{Stochastische fout}}{\text{Stochastische fout}} \gg 1\]
Als aan de aannames van de variantieanalyse (ANOVA) wordt voldaan, dan volgt de toetsinsgrootheid #F# de #F#-verdeling met # df_{model} = I-1 # vrijheidsgraden in de teller en # df_{error} = N-I # vrijheidsgraden in de noemer.

Alle #F#-verdelingen zijn rechtsscheef en het kritieke gebied van een ANOVA zal altijd in de rechterstaart van de verdeling liggen.
De #p#-waarde van de toets wordt berekend als #\mathbb{P}(F \geq f)#, waarbij #f# de waargenomen waarde van #F# is. Een kleine #p#-waarde wordt geïnterpreteerd als sterk bewijs tegen de nulhypothese en ondersteunt dus de conclusie dat de populatiegemiddelden #\mu_i# niet allemaal hetzelfde zijn, d.w.z. dat de factor een significant effect heeft op de uitkomstvariabele.
Berekening van de toetsingsgrootheid voor een enkelvoudige ANOVA
Opmerking: In de praktijk wordt de berekening van de toetsingsgrootheid #F# en de bijbehorende #p#-waarde het beste overgelaten aan statistische software, die haar bevindingen meestal samenvat in een variantieanalysetabel of ANOVA-tabel (zie hieronder).
De berekeningen van de variantie tussen steekproeven en de variantie binnen steekproeven zijn in principe precies hetzelfde als de berekening van de 'gewone' steekproefvariantie. Onthoud dat dit gebeurt door de volgende stappen uit te voeren:
- Bereken voor elke waarneming # X_i # in de steekproef de afwijking van het steekproefgemiddelde #\bar{X}#.
\[X_i-\bar{X}\] - Kwadrateer elke afwijking om te voorkomen dat positieve en negatieve afwijkingen elkaar opheffen.
\[(X_i-\bar{X})^2\] - Tel de gekwadrateerde afwijkingen bij elkaar op om een maatstaf voor de totale variabiliteit in de steekproef te creëren, de zogenaamde kwadratensom #SS#.
\[SS = \displaystyle\sum_{i=1}^n(X_i-\bar{X})^2\] - Deel de som van de kwadraten door het aantal scores in de steekproef (min #1#) om een maat te krijgen voor de gemiddelde variabiliteit per score, genaamd de gemiddelde gekwadrateerde afwijking of steekproefvariantie #s^2#.
\[s^2 = \cfrac{\displaystyle\sum_{i=1}^n(X_i-\bar{X})^2}{n-1}\]
De berekening van de varianties tussen steekproeven en binnen steekproeven komt zeer nauw overeen met het hierboven geschetste proces. In beide gevallen beginnen we met het berekenen van een maatstaf voor de totale variabiliteit, een zogenaamde kwadratensom.
De totale variabiliteit van het steekproefgemiddelde #\bar{Y}_i# rond het algemene steekproefgemiddelde #\bar{Y}#, d.w.z, de variabiliteit tussen steekproeven, wordt gemeten met de model-kwadratensom (#SS_{model}#), die wordt gegeven door:
\[SS_{model} = \displaystyle\sum^I_{i=1}n_i\Big(\bar{Y}_i - \bar{Y}\Big)^2\]
De totale variabiliteit van de waarnemingen in elke steekproef #Y_{ij}# rond hun steekproefgemiddelde #\bar{Y}_i#, d.w.z., de variabiliteit binnen steekproeven, wordt gemeten met de residuele kwadratensom (#SS_{error}#), die wordt gegeven door:
\[SS_{error} = \displaystyle\sum^I_{i=1}\displaystyle\sum^{n_i}_{j=1}\Big(Y_{ij} - \bar{Y}_i\Big)^2\]
Omdat beide metingen echter sommen zijn, hangt hun omvang sterk af van het aantal waarden dat bij de berekening wordt gebruikt. Concreet hangt de grootte van de model-kwadratensom af van het aantal steekproeven dat wordt vergeleken, en de residuele kwadratensom hangt af van het totale aantal waarnemingen in die steekproeven.
Om deze onzuiverheid te elimineren, berekenen we een gemiddelde kwadratensom.
De model-kwadratensom wordt gedeeld door de model-vrijheidsgraden (#df_{model} = I - 1 #) om de gemiddelde model-kwadratensom (# MS_{model}#) te berekenen:
\[MS_{model} = \cfrac{SS_{model}}{I - 1}\]
En de residuele kwadratensom wordt gedeeld door de residuele vrijheidsgraden (#df_{error} = N - I\, #) om de gemiddelde residuele kwadratensom (# MS_{error}#) te berekenen:
\[MS_{error} = \cfrac{SS_{error}}{N - I}\]
Ten slotte wordt de toetsingsgrootheid #F# berekend als de verhouding tussen de gemiddelde model-kwadratensom en de gemiddelde residuele kwadratensom: \[F = \cfrac{MS_{model}}{MS_{error}}\]
De resultaten van een ANOVA worden doorgaans samengevat in een ANOVA-tabel:
| ANOVA | |||||
| Uitkomstvariabele | |||||
| Kwadratensom | df | Gemiddelde kwadratensom | F | Sig. |
|
| Model | \[\displaystyle\sum^I_{i=1}n_i\Big(\bar{Y}_i - \bar{Y}\Big)^2\] | \[I-1\] | \[\cfrac{SS_{model}}{I - 1}\] | \[\cfrac{MS_{model}}{MS_{error}}\] | \[\mathbb{P}(F \geq f)\] |
| Fout | \[\displaystyle\sum^I_{i=1}\displaystyle\sum^{n_i}_{j=1}\Big(Y_{ij} - \bar{Y}_i\Big)^2\] | \[N-I\] | \[\cfrac{SS_{error}}{N - I}\] | ||
Een voorbeeld van een ANOVA-tabel gegenereerd door #\mathrm{SPSS}# zie je hieronder.
| ANOVA | |||||
| Geluksgevoel | |||||
| Sum of Squares | df | Mean Square | F | Sig. | |
| Between Groups | 0.192 | 3 | 0.064 | 1.879 | 0.142 |
| Within Groups | 2.113 | 62 | 0.034 | ||
| Total | 2.305 | 65 | |||
Op basis van deze ANOVA-tabel zouden we de nulhypothese op het significantieniveau van #\alpha = 0.01# niet verwerpen, aangezien #p > .01#, en concluderen dat de populatiegemiddelden op de verschillende niveaus van de factor allemaal gelijk zijn.
Een voorbeeld van een ANOVA-tabel gegenereerd door #\mathrm{R}# zie je hieronder.
Df Sum Sq Mean Sq F value Pr(>F)
IV 3 65 21.72 5.8 0.002 **
Residuals 36 135 3.74
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Op basis van deze ANOVA-tabel zouden we de nulhypothese op het significantieniveau van #\alpha = 0.01# verwerpen, aangezien #p < .01#, en concluderen dat de populatiegemiddelden op de verschillende niveaus van de factor niet allemaal gelijk zijn.

omptest.org als je een OMPT examen moet maken.



