Factor a quadratic

We're given the quadratic polynomial #\:q(x)#: \[ q(x)\:=\:2\cdot x^2-15\cdot x+7\hspace{0.05 cm}.\]

p (x)

The goal is to factor #\:q(x)\:# into a product of two linear terms. This problem will be accomplished in two parts. Here, in Part 1, we use the quadratic formula to calculate the roots of #\:q(x)#. #\:# And, then we check that #\:q(x)=0\:# for each of the roots found. Then, in Part 2, we will use the roots to obtain the desired factorization of #\:q(x)#.

Note. One answer per blank. So, for each blank, do not type an equal sign in your answer.

Step 1.

For the quadratic polynomial #\:q(x)\:=\:2\cdot x^2-15\cdot x+7 \:# use the quadratic formula to calculate the roots. #\:# For each root, show how to use the formula in the first blank, and simplify the answer as much as possible in the second blank. \[\small{}\mbox{tap the formula below to magnify.}\]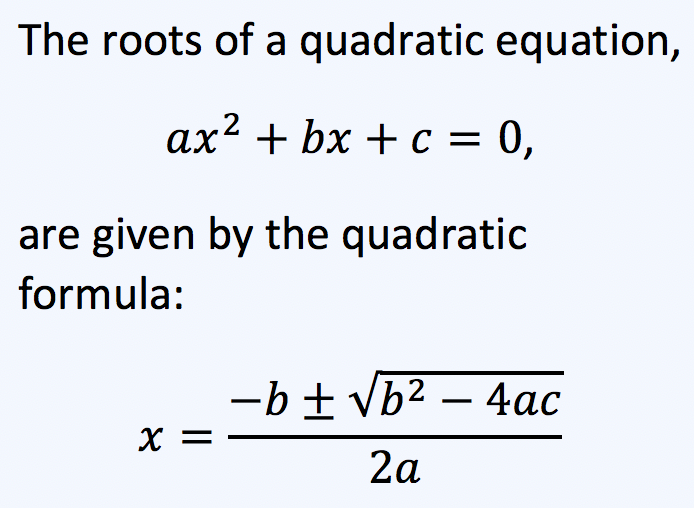

First Root #\:=\:\alpha\:=\:# #\:=\: #

Second Root #\:=\:\beta\:=\:# #\:=\: #

Step 2

Evaluate the polynomial #\:q(x)\:=\:2\cdot x^2-15\cdot x+7\:#

p (x) = 3 \cdot x^{3} + 10 \cdot x^{2} - 181 \cdot x - 252

at each of the values calculated in Step 1. For each root, show how to plug it into the polynomial for the first blank, and then simplify the result as much as possible for the second blank. Check the roots in order. So, for these calculations, make sure the first root is less than the second root: #\:\widetilde\alpha < \widetilde\beta#.

At the Lesser Root: #\:q(\widetilde\alpha)\:=\:# #\:=\:#

At the Greater Root: #\:q(\widetilde\beta)\:=\:# #\:=\:#

#\small{}\mbox{Note. If }\:q(\widetilde\alpha)\ne 0 \:\mbox{ or } \:q(\widetilde\beta)\ne 0, \: \mbox{ then re-check the calculations in Step 1 and correct any mistakes made there.}#

Edna's Math Class for OpenStax

Factor a quadratic: Factor a Quadratic: Part 1