Linear formulas and equations: Linear functions
 Composing a linear formula
Composing a linear formula
Composing a linear formula
|
Procedure |
|
|
With a graph or table of a linear formula, we can compose a formula of the form #y=\blue a \cdot x +\green b# in the following manner. |
|
| Step 1 |
Determine intercept #\green b# by seeing which #y#-value corresponds with #x=0#. |
| Step 2 |
Pick two "nice" or convenient points #A# and #B# with coordinates #\rv{x_A, y_A}# and #\rv{x_B, y_B}#. |
| Step 3 |
Calculate slope #a# with \[\blue a=\frac{y_B-y_A}{x_B-x_A}\] |
| Step 4 |
Enter the found #\blue a# and #\green b# in the formula #y=\blue a \cdot x +\green b#. |
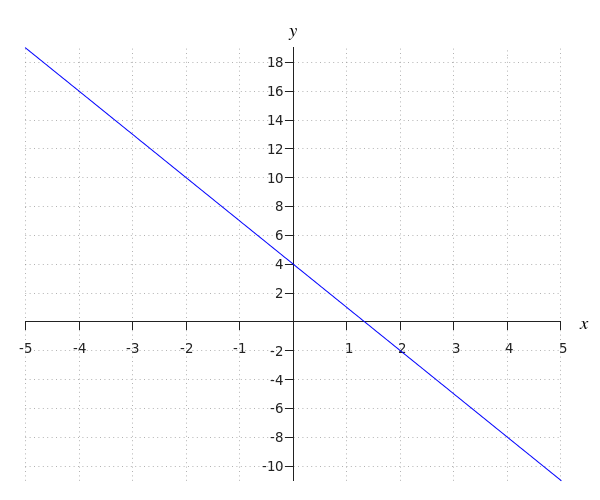
The formula is equal to #y=-3 \cdot x + 4#.
We can calculate this as follows.
Step 1: The intercept #b# is the #y#-value of the intersection point of the line and the #y#-axis. In this case, it is #4#.
Step 2: We choose two grid points, for example, #A# with coordinates #\rv{0,4}# and #B# with coordinates #\rv{2,-2}#
Step 3: We now calculate slope #a#. Here, #a=\tfrac{y_B-y_A}{x_B-x_A}=\tfrac{-2-4}{2-0}=\tfrac{-6}{2}=-3#
Step 4: We can now substitute the found values for #a# and #b# in the formula #y=a \cdot x+b#. The formula, therefore, becomes #y=-3 \cdot x + 4#.
We can calculate this as follows.
Step 1: The intercept #b# is the #y#-value of the intersection point of the line and the #y#-axis. In this case, it is #4#.
Step 2: We choose two grid points, for example, #A# with coordinates #\rv{0,4}# and #B# with coordinates #\rv{2,-2}#
Step 3: We now calculate slope #a#. Here, #a=\tfrac{y_B-y_A}{x_B-x_A}=\tfrac{-2-4}{2-0}=\tfrac{-6}{2}=-3#
Step 4: We can now substitute the found values for #a# and #b# in the formula #y=a \cdot x+b#. The formula, therefore, becomes #y=-3 \cdot x + 4#.
Unlock full access


Teacher access
Request a demo account. We will help you get started with our digital learning environment.
Student access
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.