Differentiation: Applications of derivatives
Increasing and decreasing
Increasing and decreasing
A function#f# is #\blue{\text{increasing}}# in #x# if #f(x)# increases as #x# increases.
A function #f# is #\green{\text{decreasing}}\ (dashed)# in #x# if #f(x)# decreases as #x# increases.
In the example, we see that a function can also both increase and decrease. We say that the function increases on the interval #\ivoo{-\infty}{6}# and decreases on the interval #\ivoo{6}{\infty}#.
We can check whether a function increases or decreases in a point #x# by looking at the derivative in that point.
A function #f# #\blue{\text{increases}}# in a point #x# if #f'(x)\gt 0#.
A function #f# #\green{\text{decreases}}# in a point #x# if #f'(x)\lt 0#.
A function #f# can transition from #\blue{\text{increasing}}# to #\green{\text{decreasing}}# (and the other way around) in a point #p# if #f'(p)=0#.
Example
\begin{array}{rcll}f(x)&=&x^3-8x& \text{with } f'(x)=3x^2-8\\
f'(2)&=&4&\text{therefore }f\blue{\text{ increases }}\text{in }x=2\\f'(1)&=&-5&\text{therefore }f\green{\text{ decreases }}\text{in }x=1\end{array}
| Step-by-step | Example | |
|
We want to determine the interval or intervals at which the function #f# #\blue{\text{increases}}#. |
#f(x)=\left(x-4\right)^2+6# | |
| Step 1 |
Determine the derivative of #f#. |
#f'(x)=2\left(x-4\right)# |
| Step 2 |
Determine the zeros of the derivative. |
#x=4# |
| Step 3 |
For points to the left and right of the zeros, determine whether #f'# is positive or negative. |
#f'(0)=-8# and #f'(6)=4# |
| Step 4 |
Now determine the interval / intervals on which #f# increases. The function #f# increases if #f'(x) \gt 0#. |
#f# #\blue{\text{increases}}# on #\ivoo{4}{\infty}# |
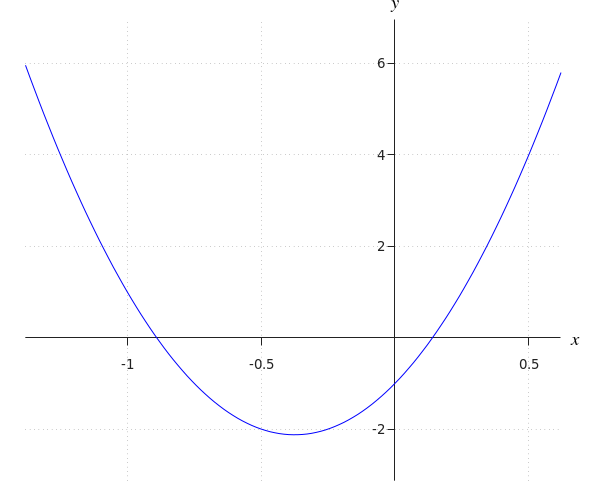
| Step 1 | We determine the derivative of #f# using the power rule. This gives: \[f'(x)=12x-3\] |
| Step 2 | We solve the equation \[12x-3=0\] This goes as follows: \[\begin{array}{rcl}12x-3&=&0 \\ &&\phantom{xxx}\blue{\text{the equation we need to solve}} \\ 12x&=&3 \\ &&\phantom{xxx}\blue{\text{both sides minus }-3} \\ x&=&\displaystyle {{1}\over{4}} \\ &&\phantom{xxx}\blue{\text{both sides divided by }12} \\\end{array}\] |
| Step 3 | #f'(-2)=-27# # f'(2)=21# |
| Step 4 | Therefore, the function #f# is decreasing on the interval #\ivoo{-\infty}{{{1}\over{4}}}# and increasing on the interval #\ivoo{{{1}\over{4}}}{\infty}#. Hence, #a={{1}\over{4}}#. |
Or visit omptest.org if jou are taking an OMPT exam.
