Direction fields

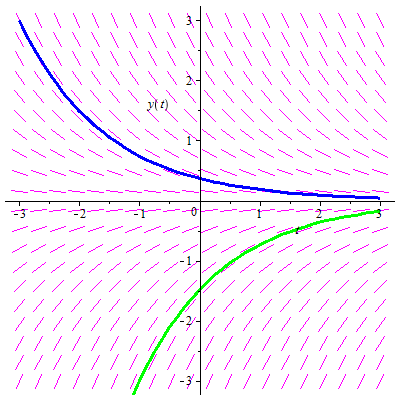
Differential equations: Direction field

Direction fields

Dynamic systems of first-order and first degree are an important class of ODEs. We will see that without performing complicated calculations you can often get an idea about the shape of the graphs of solutions of the differential equation.

Tangents to graphs of solutions of first-order ODEs of first degree

The solutions of an ODE of the form \[\frac{\dd y}{\dd t}=\varphi(t,y)\] can be interpreted geometrically as follows: Take a point \(\rv{a,b}\) and suppose that \(y(t)\) is a solution of the ODE whose graph goes through \(\rv{a,b}\). Then the tangent line to the graph of \(y\) at the point \(\rv{a,b}\) is given by the equation \[y=b+\varphi(a,b)\cdot(t-a)\]

For this function \(y\) we have \[y(a)=b\] and \[y'(a)=\frac{\dd y}{\dd t}(a)=\varphi\bigl(a,y(a)\bigr)=\varphi(a,b)\] Since #y'(a)# is the slope of the tangent line through #\rv{a,b}# to the graph of #y#, the tangent line satisfies an equation of the form \( y=\varphi(a,b)\cdot t +c\) for a constant #c#. Now #c# can be found from the equation \(b=\varphi(a,b)\cdot a +c\), which expresses the fact that the point #\rv{a,b}# is on the tangent line. The solution is #c=b-\varphi(a,b)\cdot a#. Substituting this value of #c# into the equation for the line, we find \[ y=\varphi(a,b)\cdot t +b-\varphi(a,b)\cdot a\]

Thus, the tangent line at a point \(\rv{a,b}\) of the graph of a solution \(y\) is known, even if the solution #y# itself is not known.

Direction field and solution curve

If we draw a small piece (segment) of the tangent line at the point \(\rv{a,b}\), this small line segment will be close to the solution of the ODE going through \(\rv{a,b}\). Such a segment is called a tangent element or line element at the point \(\rv{a,b}\) of the \(t,y\) plane.

Now for a variety of points \(\rv{a,b}\) in \(t,y\) plane, we can draw these line elements. A drawing with a number of these line elements is called a slope field or direction field of the ODE. Usually the points are chosen from a regular grid, but this is not necessary.

By drawing a smooth curve tangent at each point to the line elements, we obtain a so-called integral curve. This is the graph of a solution of the ODE. Such a curve is also called solution curve.

The approach of the solution curve line elements is based on the fact that the graph of a differentiable function, having a smooth pattern near all or almost all of its points, looks more and more like a straight line when we zoom in to the point. That line is the tangent line to the graph at that point.

Below the graph of a differentiable function \(f(t)\) is drawn, as well as the tangent line at the point \(\rv{a,f(a)}\). In the immediate vicinity of this point, the graph and the tangent line can hardly be distinguished from each other.

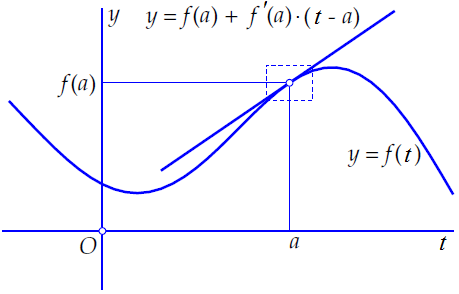
tangent line at a point of the graph

By way of illustration, the rectangle around the point \(\rv{a,f(a)}\) in the figure above is drawn again below, but enlarged.

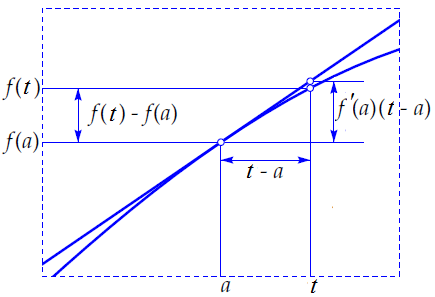
zoom in on a tangent at a point

The equation of the tangent line at the point \(\rv{a,f(a)}\) is equal to \[y=f(a)+f'(a)\cdot(t-a).\] For \(t\) near \(a\) we have: \[f(t)\approx f(a)+ f'(a)\cdot(t-a).\] This also means that if we know the value of the function and its derivative at a certain value of \(t\), we also know the function value at a small distance \(\delta\) by using the following formula: \[f(t+\delta)\approx f(t)+ f'(t)\cdot \delta\]

The closer we come to\(t\) (or: the smaller the time step \(\delta\)), the better the estimate of the function value of #f# at #t+\delta#.

Below, the direction field is shown for the differential equation \(\displaystyle\frac{\dd y}{\dd t}=r\cdot y\) with \(r=-0.7\) (so \(\varphi(t,y)=-0.7y\) ). In the figure, two integral curves are also included.

slope field

The direction field is created by drawing, at each grid point in the \(t,y\) plane, the slope of the solution by means of a small line segment. The solution with \(y(2)=1\) has derivative \(y'(2) =r \cdot y(2)=r=-0.7\) at \(t=2\). Accordingly, at the point \(\rv{2,1}\) we draw a line with slope \(-0.7\). We deal similarly with all other grid points. Note that in this example the direction field only depends on \(y\) and not on \(t\). As a consequence the drawing does not change if the image is shifted horizontally. All the time invariant (autonomous) differential equations have this property; we will discuss this later.

In this example, all the points on a horizontal line have line elements of the same direction. Such a set of points in the plane in which the line elements have the same direction is called an isoclene. The points in the plane in which the line elements have a horizontal direction, form the set of zero-isoclenes. Isoclenes are sometimes helpful in working with direction fields and considering integral curves.

In the direction field of an ODE, line elements can be vertical. The slope is equal to #\infty# then. An example is the line element at the origin of #y'(x)=\frac{1}{\sqrt{|x|}}#.

A direction field of a differential equation of first order and first degree, as well as integral curves calculated using a numerical method, often provide a good impression the solutions and their behavior.

By way of orientation we present below an interactive version of the slope field of the differential equation of logistic growth with a sigmoid (a function #\frac{1}{1+\e^{-t}}# whose graph is shaped like the letter S) as an example of one of many possible solution curves.

Drag the point \(P\) in different directions in order to see different solution curves.

You can change the settings and render a picture of the new situation by clicking the update button.

New example