Differential equations: Direction field
 Existence and uniqueness of solutions of ODEs
Existence and uniqueness of solutions of ODEs
In light of the examples that have been treated so far, it may be surprising that the domain of a solution plays a role. It is not true that a solution of an initial value problem always exists, nor need it be unique or defined for each value of the independent variable.
Two major questions in the case of initial value problems are:
- Existence: does there exist at least one solution and how far does it reach into the future and the past?
- Uniqueness: under which conditions is there at most one solution?
For first-order ODEs of the first degree, the following theorem is very useful.
Uniqueness of the solution of a first-order ODE of first degree
Suppose that the functions \(\varphi(t,y)\) and \( \displaystyle\frac{\partial \varphi(t,y)}{\partial y}\) are continuous on a rectangle \(R\) in the \(t,y\)-plane consisting of all points #\rv{t,y}#with #a\lt t\lt b# and #c\lt y \lt d# for given constants #a#, #b#, #c#, #d#, and that \(\rv{t_0,y_0}\) is a point of \(R\). Then the initial value problem \[\frac{\dd y}{\dd t}=\varphi(t,y)\]
- (existence) has a solution \(y(t)\) on a certain interval for #t# containing \(t_0\) and contained in the open interval \(\ivoo{a}{b}\),
- (uniqueness) has no more than one solution on an open interval within the interval of the existence statement containing \(t_0\).
We will devote a lot of attention to the linear first-order differential equation: \[y' +p(t)\cdot y =q(t)\] If the functions #p(t)# and #q(t)# are continuous on an open interval #\ivoo{a}{b}# met #a\lt t_0\lt b#, then the conditions of the theorem are satisfied for the rectangle #R# of all points #\rv{t,y}# with #a\lt t\lt b#. Indeed \(\varphi(t,y)=q(t)-p(t)\cdot y\) is continuous on #R# since \(p(t)\cdot y\) is the product of the continuous functions #p(t)# of #t# and #y# of #y# (the identity function), and \( \displaystyle\frac{\partial \varphi(t,y)}{\partial y}=-p(t)\) is continuous on \(R\). Later we will see that in this case existence and uniquess hold on the whole interval #\ivoo{a}{b}#, and further on we will even provide an explicit expression for the solution, up to the computation of two antiderivatives.
The open interval around #t_0# on which the unique solution of the above statement can be found, can be chosen as widely as possible. If this is the case, we speak of the the interval of validity of the initial value problem.
Even if existence and uniqueness are guaranteed, it is still an interesting matter to determine the maximum interval at which the solution of an initial value problem exists. This maximum existence interval often depends on the choice of initial value. In other words, the theorem is about local existence: solutions of an initial value problem are not necessarily defined for all values of \(t\).
We require that the interval of validity be open.
If the conditions in the statement above are not met, existence and uniqueness may be a problem. Three examples are given below, showing
- multiple solutions of an initial value problem,
- explosive solutions and multiple solutions for the price of one formula,
- solutions that come to a halt.
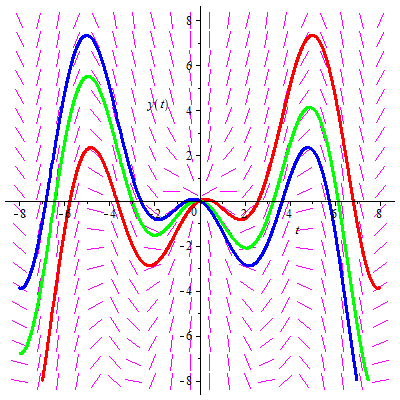
\(t\cdot \frac{\dd y}{\dd t}=y-t^2\cdot\cos(t),\quad y(0)=0\)
We begin by rewriting this initial value problem in the form used in the statement of the theorem on existence and uniqueness: \[\frac{\dd y}{\dd t}=\frac{y}{t}-t\cdot\cos(t)\]This only works if \(t\neq 0\). So problems with existence and uniqueness may only occur at \(t=0\). An exact slution to the differential equation can be given, which helps to sort out what is going on. First write the above ODE in the following form: \[\frac{y'\cdot t-y}{t^2}=-\cos(t)\] According to the quotient rule for differentiation, the left-hand side of this equation is the derviative of \(\frac{y}{t}\). The right-hand side can be written as the derivative of \(-\sin(t)\). Therefore: \[ \frac{\dd}{\dd t}\left( \frac{y}{t} \right)=\frac{\dd}{\dd t}\left(-\sin(t)\right) \] The derivatives on both sides are equal and so the two sides should differ by a constant: \[\frac{y}{t}=C-\sin( t)\] or \[y=C\cdot t-t\cdot\sin( t)\] for a certain constant \(C\). Substitution of this solution into the ODE shows that this function is defined everywhere and a solution indeed for all #C#. For each choice of the constant we have \(y(0)=0\). In particular, the initial value problem has an infinite number of solutions.
In the figure below, some solution curves of this initial value problem are shown along with the direction field.

Or visit omptest.org if jou are taking an OMPT exam.



