Differential forms and separated variables

Differential equations: Separation of variables

Differential forms and separated variables

We have seen that finding an antiderivative of the function #f(t)# can be formulated as solving the first order differential equation #y'=f(t)#. An effective intermediate step from the ODE to the solution turned out to be its differential form: #\dd y = f(t)\,\dd t#. There are more first-order ODEs that can be solved using differential forms.

Separation of variables

Suppose that \(f(t)\) and \(g(y)\) are continuous functions, that #g(y)# is not the constant function #0#, that \(F(t)\) is an anti-derivative of #f(t)#, and that \(H(y)\) an anti-derivative of #\frac{1}{g(y)}#.

The general solution #y# of the differential equation \[y'(t)={g(y)}\cdot {f(t)}\] satisfies the equality \[H(y)=F(t)+C\] where \(C\) is a constant.

The differential equation \[\frac{\dd y}{\dd t} = {g(y)}\cdot{f(t)} \] can be written in differential form as \[\dfrac{1}{ g(y)}\,\dd y = f(t)\,\dd t\] and so it is equivalent to \[\dd\bigl(H(y)\bigr) = \dd\bigl(F(t)\bigr)\] Consequently, \[H(y)=F(t)+C\] for a constant \(C\).

If #g(y)# is the constant function #0#, then the left hand side of the ODE is equal to #0#, so #y# is a constant function. This case is easy to handle.

In general, this is not a solution of the ODE in the explicit form \( y(t)=\text{a function of }t\), but a relationship between the variables \(y\) and \(t\). Sometimes you can derive an explicit solution from this relationship.

Separable differential equation

Let #y# be a differentiable function of #t#. A separable differential equation is a first order differential equation of first degree in which the derivative \(y'\) can be factored as a product of a function \(g(y)\) of the unknown dependent variable \(y\) and a function \(f(t)\) of the independent variable \(t\): \[ y'(t) =g(y) \cdot f(t) \]

A solution such as #H(y)=F(t)+C# of the above theorem is often referred to as an implicit solution of the ODE.

If there are initial conditions, the implicit solution can be used for finding corresponding values of #C#.

Each autonomous ODE is separable. After all, such an ODE can be written as \(y '(t) = g(y) \cdot f(t)\) with #f(t)# equal to the constant function #1#.

Below are some examples. Later we will discuss the method in greater detail and provide more examples.

Determine a function #y# of #t# having value #1# at #0# that satisfies the ODE \[y' =\dfrac{1}{3} \]

#y= \dfrac{1}{3}\; t + 1#

The differential equation is separable since, putting \(g(y) = \frac{1}{3} \) and \(f(t) = 1 \), we can rewrite it as
\[ 3\; \dd y = 1\; \dd t \]
After computing antiderivatives we have
\[ 3 y = t + C \]
Multiplying both sides by \(\frac{1}{3}\), we find
\[ y = \dfrac{1}{3}\; t + C \]
This is the general solution of the differential equation.

This solution denotes a class of functions, all of which have a rate of growth one third. Geometrically, we can represent the class of functions with the following slope field.

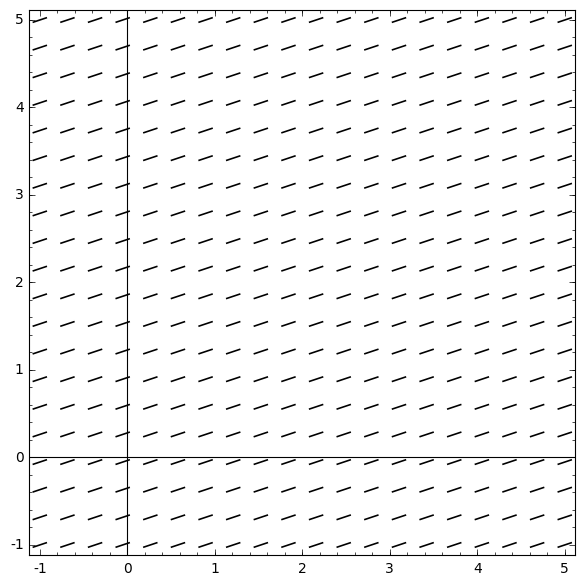
To obtain a specific solution we proceed to solve initial value problem with the initial condition \(\rv{t,y} = \rv{0,1}\). After substituting the values \(y=1\) and \(t=0\) we find
\[ 1 = \dfrac{1}{3}\; \cdot 0 + C \]
Therefore we have \(C = 1\), so the corresponding specific solution is the function:
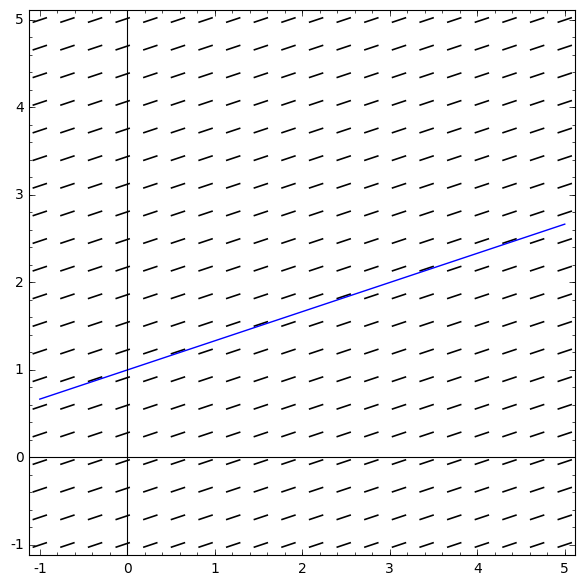
\[ y = \dfrac{1}{3}\; t + 1 \]
This is represented graphically as a line inside the slope field.

New example