Hoofdstuk 1: Beschrijvende statistiek: Centrummaten
Mediaan
De mediaan is het middelpunt van een verdeling, wat betekent dat deze score de verdeling in twee gelijke helften opsplitst.
De mediaan is gelijk aan het #50^{e}# percentiel, wat betekent dat precies #50\%# van de scores in een verdeling gelijk zijn aan of kleiner zijn dan de mediaan.
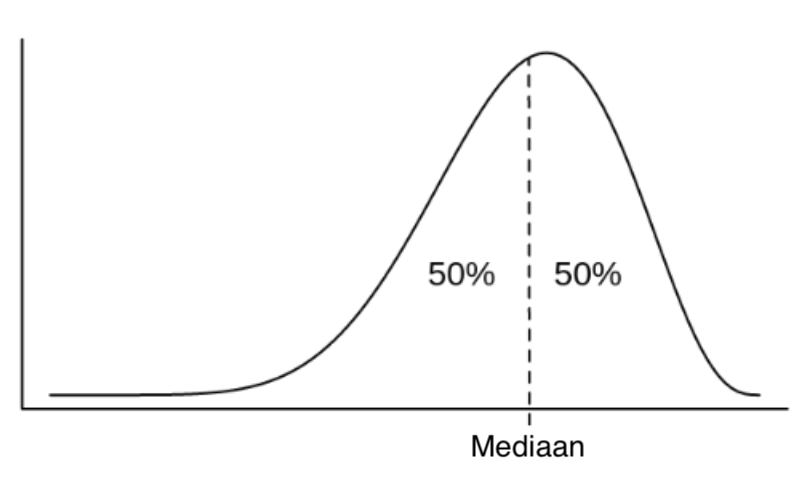
Mediaan berekening
Om de mediaan te berekenen, sorteren we eerst de scores in oplopende of aflopende volgorde.
Vervolgens bepalen we of verdeling bestaat uit een oneven of even aantal scores.
- Als de verdeling bestaat uit een oneven aantal scores, dan is de mediaan de middelste score in de lijst van gesorteerde scores. Deze score zal staan op de #(\cfrac{n+1}{2})#e positie van de lijst.
- Als de verdeling bestaat uit een even aantal scores, dan is de mediaan de waarde die halverwege de middelste twee scores ligt. Deze middelste scores bevinden zich op de #(\cfrac{n}{2})#e en de #(\cfrac{n}{2} + 1)#e positie van de lijst.
#\text{Mediaan}=13#
Er bestaan een aantal manieren op de mediaan te berekenen. Klik op één van de panelen om de desbetreffende oplossing te bekijken.
Om de mediaan te berekenen, sorteren we eerst de scores in oplopende of aflopende volgorde.
\[2,\,\,\,2,\,\,\,3,\,\,\,6,\,\,\,11,\,\,\,13,\,\,\,14,\,\,\,16,\,\,\,18,\,\,\,18,\,\,\,19\]
De steekproef bestaat uit #n=11# scores.
Aangezien er een oneven aantal scores in de steekproef zitten, is de mediaan gelijk aan de middelste score van de geordende lijst.
Voor een steekproef van #11#, staat de middelste score op de #(\cfrac{n+1}{2})=\cfrac{11+1}{2}=6#e positie:\[\text{Mediaan} = X_{6} = 13\]
Ervantuigaande dat de scores in cel A1 tot en met A11 staan, moeten we dus het volgende Excel commando uitvoeren:MEDIAN(array)
- array: De reeks of celbereik van numerieke waarden waarvoor je de mediaan wilt berekenen.
\[= \text{MEDIAN(A1:A11)}\]
Dit geeft
\[\text{Mediaan} = 13\]
Het R commando om de mediaan te berekenen is dus:median(x)
- x: De numerieke vector waarvan je de mediaan wilt berekenen.
\[median(x = c(2,16,2,11,19,14,3,13,6,18,18))\]
Dit geeft:
\[\text{Mediaan}=13\]
Omdat de berekening van de mediaan vereist dat de data geordend kan worden, kan de mediaan niet berekend worden voor nominale data.
\[
\begin{array}{c|cccc}
&\text{Nominaal}&\text{Ordinaal}&\text{Interval}&\text{Ratio}\\
\hline
\text{Modus}&\green{\text{Ja}}&\green{\text{Ja}}&\green{\text{Ja}}&\green{\text{Ja}}\\
\text{Mediaan}&\red{\text{Nee}}&\green{\text{Ja}}&\green{\text{Ja}}&\green{\text{Ja}}\\
\end{array}
\]
omptest.org als je een OMPT examen moet maken.
