Setting the Criteria for a Decision

Chapter 7. Hypothesis Testing: Introduction to Hypothesis Testing (p-value Approach)

Setting the Criteria for a Decision

Once the hypotheses of the test have been formulated, the next step is to set the criteria for a decision. This should always be done before the sample data is collected.

Specifically, we need to determine what values of the sample statistic will lead to the rejection of the null hypothesis. Because a sample provides an incomplete picture of a population, some discrepancy between a sample statistic and its corresponding population parameter is to be expected.

How much discrepancy is reasonable to expect can be derived from the sampling distribution of the sample statistic under the null hypothesis. If the null hypothesis is true, it is likely that the sample statistic will be relatively close in value to the mean of the sampling distribution.

As the difference between a sample statistic and the mean of the hypothesized sampling distribution increases, your confidence in the null hypothesis being true should decrease. If you observe a sample statistic that is extremely unlikely to occur given that the null hypothesis is true, this should lead to the rejection of the null hypothesis.In order to formalize what constitutes as an extremely unlikely result, the significance level of the test needs to be set.
#\phantom{0}#

Significance level

The significance level, denoted #\alpha#, of a statistical test is the probability threshold that determines how unlikely a sample statistic has to be in order for the null hypothesis #H_0# to be rejected.

The range of values for the sample statistic that will lead to the rejection of the null hypothesis is called the critical region. The boundary values of the critical region are called critical values.

Decreasing the significance level shrinks the critical region of the sampling distribution, meaning a smaller range of values will lead to the rejection of #H_0#.

Increasing the significance level expands the critical region of the sampling distribution, meaning a larger range of values will lead to the rejection of #H_0#.

Significance Level Interactive

Setting an #\alpha = 0.05# significance level means that if you observe a sample statistic that has a #5\%# or less chance of occurring if the null hypothesis is true, the null hypothesis should be rejected.

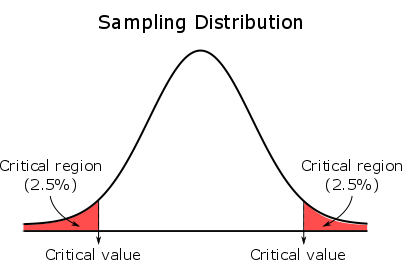
For a two-tailed test, the critical region is evenly split between both tails.

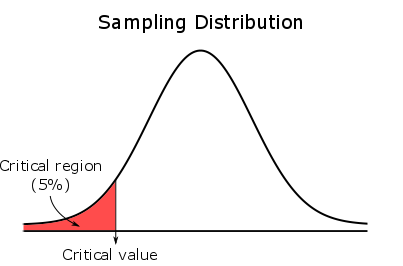
For a left-tailed test, the entire critical region is located in the left tail.

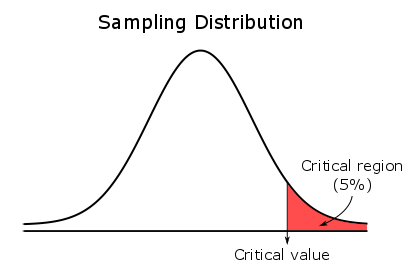
For a right-tailed test, the entire critical region is located in the right tail.

Choosing an Appropriate Significance level

Note that the choice of the significance level #\alpha# should be made with care. The stronger the alternative hypothesis, the smaller #\alpha# should be.

For example, #H_a: \mu \gt \mu_0# is a stronger hypothesis than #H_a: \mu \neq \mu_0#, because the former hypothesis not only specifies that #\mu# is different from #\mu_0# but also that #\mu# differs from #\mu_0# in a specific direction. So a smaller #\alpha# should be used for a one-tailed test than what is used for a two-tailed test.

An additional consideration is the severity of the consequences if a conclusion is made in favor of #H_a#, but this decision turns out to be a mistake. If severe harm could be caused (e.g. damage to someone's health, loss of large sums of money), then a smaller #\alpha# should be used.

On the other hand, using an #\alpha# that is too small could also have severe consequences, because concluding in favor of #H_0# when #H_a# is actually true might could for example lead to the failure to provide a treatment for an illness that would have been effective.