Chapter 7. Hypothesis Testing: Hypothesis Test for a Population Proportion
 Large-sample Proportion Test: Test Statistic and p-value
Large-sample Proportion Test: Test Statistic and p-value
Suppose we draw a simple random sample of size #n# from a population of which some proportion #\pi# exhibits a particular characteristic.
Let #X# denote the number of successes out of #n# observations, and let #\hat{p}=\frac{X}{n}# denote the sample proportion.
When the sample size is large (#n\geq 30#), the Central Limit Theorem can be invoked, and a #Z#-test can be used to test certain hypotheses about the population proportion #\pi#.
#\phantom{0}#
Z-test for a Population Proportion: Test Statistic
The test statistic of a #Z#-test for a population proportion #\pi# is calculated as follows:
\[Z=\cfrac{\hat{p}-\pi_0}{\sigma_{\hat{p}}}=\cfrac{\hat{p}-\pi_0}{\sqrt{\pi_0 \cdot (1 - \pi_0)/n}}\]
Under the assumption that the null hypothesis #H_0# is true, the sampling distribution of #Z# is the Standard Normal Distribution. That is, #Z \sim N(0,1)#.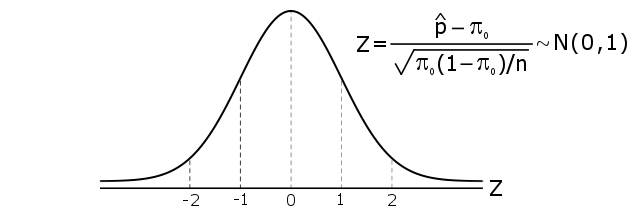
A lowercase #z# will be used to denote the measured value of #Z# after the data has been collected.
Calculating the p-value of a Z-test for a Population Proportion with Statistical Software
The calculation of the #p#-value of a #Z#-test for #\pi# is dependent on the direction of the test and can be performed using either Excel or R.
To calculate the #p#-value of a #Z#-test for #\pi# in Excel, make use of one of the following commands:
\[\begin{array}{lllll}
\phantom{0}\text{Direction}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-value}&\phantom{0000000000}\text{Excel Command}\\
\hline
\text{Two-tailed}&H_0:\pi = \pi_0&H_a:\pi \neq \pi_0&2\cdot \mathbb{P}(Z\geq |z|)&=2 \text{ * }(1 \text{ - }\text{NORM.DIST}(\text{ABS}(z),0,1,1))\\
\text{Left-tailed}&H_0:\pi \geq \pi_0&H_a:\pi \lt \pi_0&\mathbb{P}(Z\leq z)&=\text{NORM.DIST}(z,0,1,1)\\
\text{Right-tailed}&H_0:\pi \leq \pi_0&H_a:\pi \gt \pi_0&\mathbb{P}(Z\geq z)&=1 \text{ - }\text{NORM.DIST}(z,0,1,1)\\
\end{array}\]
To calculate the #p#-value of a #Z#-test for #\pi# in R, make use of one of the following commands:
#\begin{array}{lllll}
\phantom{0}\text{Direction}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-value}&\phantom{000000}\text{R Command}\\
\hline
\text{Two-tailed}&H_0:\pi = \pi_0&H_a:\pi \neq \pi_0&2\cdot \mathbb{P}(Z\geq |z|)&2 \text{ * }\text{pnorm}(\text{abs}(z),0,1, \text{FALSE})\\
\text{Left-tailed}&H_0:\pi \geq \pi_0&H_a:\pi \lt \pi_0&\mathbb{P}(Z\leq z)&\text{pnorm}(z,0,1, \text{TRUE})\\
\text{Right-tailed}&H_0:\pi \leq \pi_0&H_a:\pi \gt \pi_0&\mathbb{P}(Z\geq z)&\text{pnorm}(z,0,1, \text{FALSE})\\
\end{array}#
If #p \leq \alpha#, reject #H_0# and conclude #H_a#. Otherwise, do not reject #H_0#.
Note: #|z|# denotes the absolute value of #z#, i.e. the distance of #z# from #0#, regardless of whether #z < 0# or #z > 0#.
To test this claim, a journalist working at a newspaper surveys #95# citizens, using random sampling. Let #X# denote the number of citizens who are in favor of the new law.
The journalist plans on using a hypothesis test to determine if the proportion of citizens who are in favor of the new law significantly differs from #0.65#, at the #\alpha = 0.01# level of significance.
The survey results indicate that #71# of the citizens in the sample are in favor of the new proposal.
Calculate the #p#-value of the test and make a decision regarding #H_0: \pi = 0.65#. Round your answer to #4# decimal places.
On the basis of this #p#-value, #H_0# should not be rejected, because #\,p# #\gt# #\alpha#.
There are a number of different ways we can calculate the #p#-value of the test. Click on one of the panels to toggle a specific solution.
A sample size of #95# is considered large enough for the Central Limit Theorem to apply. This means that the test statistic
\[Z=\cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0 \cdot (1-\pi_0) / n}}\]
approximately has the #N(0,1)# distribution under the assumption that #H_0# is true.
Compute the sample proportion #\hat{p}#:
\[\hat{p} = \cfrac{X}{n} = \cfrac{71}{95} = 0.74737\]
Calculate the value of test statistic #z#:
\[z = \cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0\cdot(1-\pi_0)/n}} = \cfrac{0.74737 - 0.65}{\sqrt{0.65\cdot(1 - 0.65) / 95}} = 1.98971\]
For a two-tailed #Z#-test, the #p#-value is defined as #2\cdot \mathbb{P}(Z \geq |z|)#. To calculate this value in Excel, make use of the following function:
NORM.DIST(x, mean, standard_dev, cumulative)
- x: The value at which you wish to evaluate the distribution function.
- mean: The mean of the distribution.
- standard_dev: The standard deviation of the distribution.
- cumulative: A logical value that determines the form of the function.
- TRUE - uses the cumulative distribution function, #\mathbb{P}(X \leq x)#
- FALSE - uses the probability density function
Thus, to calculate #p = 2\cdot \mathbb{P}(Z \geq |z|)#, run the following command:
\[
=2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(z),0,1,1))\\
\downarrow\\
=2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(1.98971),0,1,1))
\]
This gives:
\[p = 0.0466\]
Since #\,p# #\gt# #\alpha#, #H_0: \pi = 0.65# should not be rejected.
A sample size of #95# is considered large enough for the Central Limit Theorem to apply. This means that the test statistic
\[Z=\cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0 \cdot (1-\pi_0) / n}}\]
approximately has the #N(0,1)# distribution under the assumption that #H_0# is true.
Compute the sample proportion #\hat{p}#:
\[\hat{p} = \cfrac{X}{n} = \cfrac{71}{95} = 0.74737\]
Calculate the value of test statistic #z#:
\[z = \cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0\cdot(1-\pi_0)/n}} = \cfrac{0.74737 - 0.65}{\sqrt{0.65\cdot(1 - 0.65) / 95}} = 1.98971\]
For a two-tailed #Z#-test, the #p#-value is defined as #2\cdot \mathbb{P}(Z \geq |z|)#. To calculate this value in R, make use of the following function:
pnorm(q, mean, sd, lower.tail)
- q: The value at which you wish to evaluate the distribution function.
- mean: The mean of the distribution.
- sd: The standard deviation of the distribution.
- lower.tail: If TRUE (default), probabilities are #\mathbb{P}(X \leq x)#, otherwise, #\mathbb{P}(X \gt x)#.
Thus, to calculate #p = 2\cdot \mathbb{P}(Z \geq |z|)#, run the following command:
\[
2 \text{ * } \text{pnorm}(q = \text{abs}(z), mean = 0, sd = 1,lower.tail = \text{FALSE})\\
\downarrow\\
2\text{ * } \text{pnorm}(q = \text{abs}(1.98971), mean = 0, sd = 1,lower.tail = \text{FALSE})
\]
This gives:
\[p = 0.0466\]
Since #\,p# #\gt# #\alpha#, #H_0: \pi = 0.65# should not be rejected.

Or visit omptest.org if jou are taking an OMPT exam.



