Enkelvoudige variantieanalyse in R
Data en onderzoeksvraag

Het statistische softwarepakket #\mathrm{R}# kan worden gebruikt om efficiënt een enkelvoudige variantieanalyse uit te voeren. We demonstreren dit met behulp van de volgende data, die je kunt kopiëren en plakken in #\mathrm{R}# :

 Y <- c(25.6,22.8,27.5,21.3,23.0,33.4,25.2,19.6,29.4,20.8,32.7,23.3,18.2,28.7,24.0)

 Group <- c(2,1,3,1,2,3,2,1,3,1,3,2,1,3,2)

 Data <- data.frame(Y, Groep)

Hier is #\mathtt{Y}# de uitkomstvariabele en #\mathtt{Group}# de categorische factor, die 3 niveaus heeft. Er zijn #15# waarnemingen, en positie #k# in de twee vectoren geeft het niveau van de factor en de waarde van de uitkomstvariabele voor het #k#-de subject, voor #k = 1,...,15#.

We voegen deze samen in een data frame dat we voor het gemak #\mathtt{Data}# noemen. (Als je gegevens in #\mathrm{R}# leest vanuit een bestand met behulp van de #\mathtt{read.table()}#-functie, worden deze geladen als een data frame. Je kunt er elke gewenste naam aan geven, hoewel Data vaak het meest logisch is.)

De onderzoeksvraag die we willen beantwoorden is: Is het populatiegemiddelde van de uitkomstvariabele #Y# voor alle drie de groepen hetzelfde?

---

Enkelvoudige variantieanalyse

Om de nulhypothese van gelijke populatiegemiddelden te toetsen, maken we eerst het variantieanalyse-model met behulp van de #\mathtt{aov()}#-functie.

 > Model <- aov(Y ~ factor(Group), data = Data)

We slaan de output van de #\mathtt{aov()}#-functie op in een object dat we #\mathtt{Model}# noemen. Je kunt elke naam kiezen die je wilt.

Merk ook op dat we de numeric vector #\mathtt{Group}# moeten converteren naar de factor class met behulp van de #\mathtt{factor()}#-functie, als we willen dat de #\mathtt{aov()}#-functie correct werkt. Zelfs als #\mathtt{Group}# zich al in de factor class bevond, zou het gebruik van de functie #\mathtt{factor()}# geen kwaad kunnen, dus voor de zekerheid is het een goed idee om dit altijd te doen.

Merk ook op dat de functie #\mathtt{aov()}# ons in staat stelt het data frame te specificeren waarin we de variabelen kunnen vinden, zodat we niet #\mathtt{Data$Y}# en #\mathtt{Data$Group}# hoeven te typen. Als de variabelen niet in een data frame zijn genest, maar in de #\mathrm{R}# work space, dan zouden we de "#\mathtt{data=}#"-instelling niet gebruiken.

Om de steekproefgemiddelden samen met het algemene steekproefgemiddelde te inspecteren, gebruiken we de #\mathtt{model.tables()}#-functie op het object #\mathtt{Model}#, met het argument #\mathtt{type=}# "#\mathtt{means}#":

> model.tables(Model, type = "means")
Tables of means 
Grand mean 

25.03333 

 factor(Group) 
factor(Group) 
 1 2 3 
20.54 24.22 30.34 

Nu het variantieanalyse-model is geconstrueerd, gebruiken we de functie #\mathtt{summary()}# op het object #\mathtt{Model}# om de resultaten van de analyse te inspecteren:

> summary(Model)
 Df Sum Sq Mean Sq F value Pr(>F) 
factor(Group) 2 245.06 122.53 33.47 1.23e-05 *** 
Residuals 12 43.93 3.66 
--- 
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

De output van de functie #\mathtt{summary()}# is een variantieanalyse-tabel. Hier is de gegeven #p#-waarde #p=0.0000123#, wat tussen #0# en #0.001# ligt, zoals aangegeven door de #3# sterren naast de waarde.

We zouden de nulhypothese verwerpen en concluderen dat er, van de drie groepen, ten minste twee populatiegemiddelden zijn die verschillen. Deze conclusie is echter alleen geldig als aan de aannames is voldaan.

---

Het controleren van de aannames

Als de conclusie van de enkelvoudige variantieanalyse is dat de nulhypothese van gelijke gemiddelden wordt verworpen, dan zijn er twee aannames die we moeten controleren voordat we verder gaan met de post hoc-analyse:

• De aanname van normaliteit wordt gecontroleerd door te bepalen of de residuen van het model al dan niet normaal verdeeld zijn.

• De aanname van homogeniteit van varianties wordt gecontroleerd door te bepalen of de variantie van de residuen al dan niet voor alle groepen hetzelfde is.

In beide gevallen maken we eerst een spreidingsdiagram om een eerste indruk van de situatie te krijgen, voordat we overgaan tot een formele test van de aanname.

Om de normaliteit van de uitkomstvariabele #\mathtt{Y}# in elke groep visueel te inspecteren, maken we een Q-Q plot van de model-residuen:

> qqnorm(Model$residuals, pch=20)

> qqline(Model$residuals)

De eerste functie #\mathtt{qqnorm()}# tekent het spreidingsdiagram en de tweede functie #\mathtt{qqline()}# creëert de referentielijn. Hierdoor ontstaat de volgende Q-Q plot: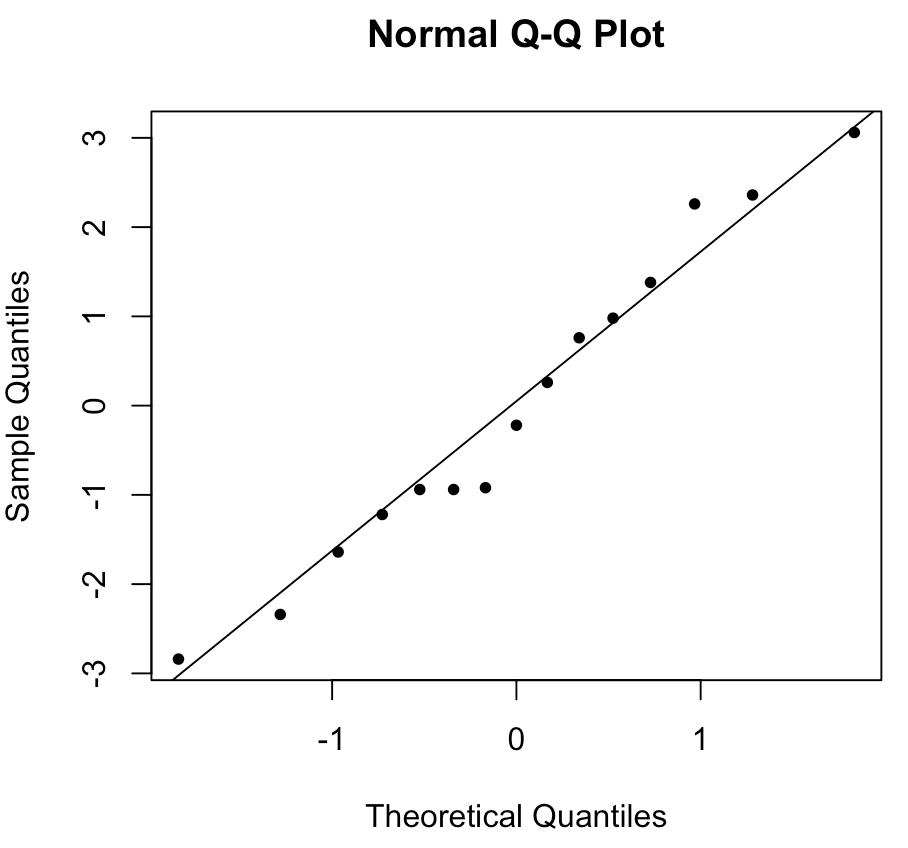

In dit geval liggen de punten zo dicht bij de lijn dat we er redelijk zeker van kunnen zijn dat aan de aanname van normaliteit is voldaan.

Om er zeker van te zijn dat de aanname van normaliteit niet wordt geschonden, voeren we vervolgens de Shapiro-Wilk-toets uit om de volgende hypothesen formeel te testen:
\[\begin{array}{rcl}
H_0&:&\text{De residuen zijn normaal verdeeld.}\\\\
H_a&:&\text{De residuen zijn niet normaal verdeeld.}
\end{array}\] Om de toets uit te voeren, gebruiken we de #\mathtt{shapiro.test()}#-functie op de residuen van het object #\mathtt{Model}#:

> shapiro.test(Model$residuals)

 Shapiro-Wilk normality test
 
data: Model$residuals 
W = 0.96597, p-value = 0.7945

De #p#-waarde van #p=0.7945# is zo groot dat de nulhypothese van de test op geen enkel redelijk significantieniveau #\alpha# verworpen zou worden. We kunnen dus concluderen dat aan de normaliteitsaanname is voldaan.

Om de variantie van de residuen visueel te inspecteren, maken we een spreidingsdiagram van de modelresiduen tegen de gefitte waarden (d.w.z. de groeps-steekproefgemiddelden):

> plot(Model$fitted.values, Model$residuals, pch=20, xlab="Fitted values", ylab="Residuals")

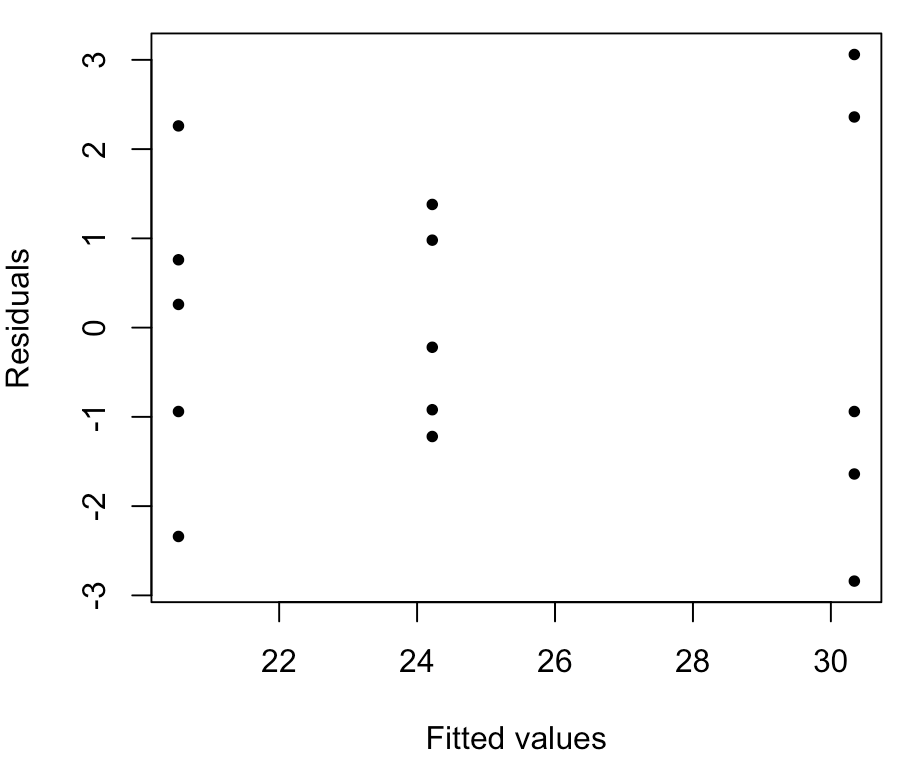
Hier is de spreiding van de punten in de middelste groep (groep 2) merkbaar kleiner dan de spreiding van de punten in de andere twee groepen, wat erop wijst dat we mogelijk een probleem hebben met de aanname van gelijke varianties. Dit is visueel echter lastig aan te pakken.

Om de homogeniteitsaanname formeel te beoordelen, gebruiken we Bartlett's toets om de volgende hypothesen te testen:
\[\begin{array}{rcl}
H_0&:&\text{De populatievarianties zijn allemaal gelijk.}\\\\
H_a&:&\text{De populatievarianties zijn niet allemaal gelijk.}
\end{array}\] Om de toets uit te voeren, gebruiken we de #\mathtt{bartlett.test()}#-functie, die dezelfde invoer nodig heeft als de #\mathtt{aov()}#-functie die we eerder gebruikten:

> bartlett.test(Y ~ factor(Group), data = Data) 

Bartlett test of homogeneity of variances 

data: Y by factor(Group) 
Bartlett's K-squared = 2.2327, df = 2, p-value = 0.3275

De #p#-waarde van #p=0.3275# is zo groot dat de nulhypothese van de toets bij geen enkel redelijk significantieniveau #\alpha# verworpen zou worden. We kunnen dus concluderen dat aan de aanname van homogeniteit van varianties is voldaan.

---

Post hoc-analyse

De laatste stap van de variantieanalyse-procedure is het uitvoeren van een post hoc-analyse om te bepalen welke populatiegemiddelden van elkaar verschillen.

Omdat aan de aanname van gelijke populatievarianties is voldaan, wordt de Tukey-Kramer-toets (Engels: Tukey-Kramer HSD test) aanbevolen. Om deze toets uit te voeren, gebruiken we de #\mathtt{TukeyHSD()}#-functie, die het object #\mathtt{Model}# als invoer gebruikt:

> TukeyHSD(Model)
Tukey multiple comparisons of means
95% family-wise confidence level 

Fit: aov(formula = Y ~ factor(Group), data = Data) 

$`factor(Group)`
diff lwr upr p adj
2-1 3.68 0.4515543 6.908446 0.0257595
3-1 9.80 6.5715543 13.028446 0.0000092
3-2 6.12 2.8915543 9.348446 0.0007588

Als we een significantieniveau van #\alpha = 0.01# gebruiken, zouden we concluderen dat er een significant verschil bestaat tussen de populatiegemiddelden van de groepen #1# en #3# en tussen de gemiddelden van de groepen #2# en #3#, maar niet tussen de gemiddelden van de groepen #1# en #2#.