Functies en grafieken

Functies: Functies

Functies en grafieken

Tot nu toe hebben we een functie vaak getoond met behulp van een functievoorschrift, maar het is vaak handig om een functie visueel weer te geven. Dit doen we met grafieken.

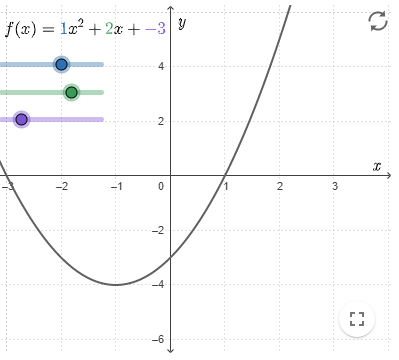
De grafiek van een kwadratische functie is een parabool.

De afbeelding rechts is de grafiek van de functie \[f(x)=\blue ax^2+\green bx+\purple c\]

Door de schuifregelaars te gebruiken kunnen de waarden van #\blue a#, #\green b# en #\purple c# worden gewijzigd.

Als de functie verandert, dan verandert de grafiek mee. De grafiek laat visueel zien hoe de functie eruitziet.

Na dit voorbeeld van de grafiek van een functie zullen we een formele definitie bespreken.

Grafiek

De grafiek van een functie #f : \blue X \to \orange Y# is de verzameling

\[\{\rv{\blue x,\orange{f(x)}} \mid \blue x \in \blue X\}\]

Dit is een deelverzameling van #\blue X \times \orange Y#.

Voor een reële functie #f\colon\blue X \to \orange{\mathbb{R}}# met #\blue X \subseteq \mathbb{R}# is de grafiek van een functie een deelverzameling van het vlak #\mathbb{R}^2#.

Gebruik van y

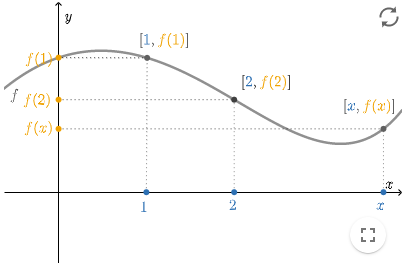
Zoals we in de bovenstaande grafiek al zagen, tekenen we de grafiek van een reële functie vaak op een #xy# -vlak. De grafiek is de verzameling punten #\rv{x,y}# op het vlak waarvoor geldt dat #y=f(x)#.

Punten aflezen

Voor een reële functie #f# kunnen we de waarde van #f(x)# van de grafiek aflezen door de hoogte van de grafiek boven het punt #x# te bepalen, zoals hierboven wordt aangegeven.

Een grafiek kan ook helpen om het domein en het bereik van een functie te bepalen.

Lineaire functie

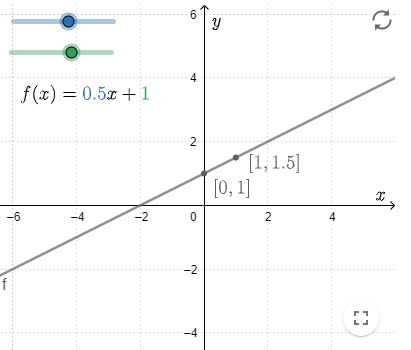
Een lineaire functie heeft de vorm #f(x)=\blue a x+\green b# met de getallen #\blue a# en #\green b#. De grafiek van deze functie is een rechte lijn.

De helling van deze lijn wordt bepaald door de richting van de coëfficiënt #\blue a#.

Ook weten we dat deze lijn door het punt #\rv{0,\green b}# gaat.

Stuksgewijs gedefinieerde functie

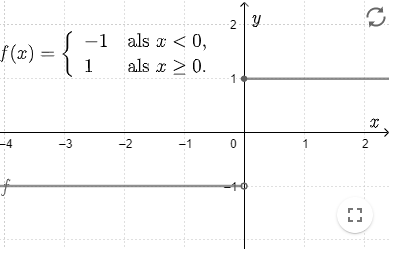
In de grafiek van een stuksgewijs gedefinieerde functie hebben we vaak een sprong in de grafiek (zie figuur rechts).

We gebruiken dan een open cirkel om aan te geven dat het punt zelf geen deel uitmaakt van de grafiek, maar alle punten van de lijn in de buurt van dat punt wel.

We gebruiken een dichte cirkel om aan te geven dat het punt zelf ook deel uitmaakt van de grafiek.

Histogrammen

Op het gebied van statistiek wordt de term histogram gebruikt. Een histogram is een diagram van de frequentieverdeling van gegevens die zijn gegroepeerd in klassen. De leeftijd van een groep van #100# leerlingen kan bijvoorbeeld worden weergegeven in een histogram, zoals in de afbeelding rechts.

Een histogram kan ook worden gezien als de grafiek van een functie. In het bovenstaande voorbeeld, met betrekking tot het aantal leerlingen per leeftijdsgroep in een groep van #100# studenten, laat de functie zien hoeveel studenten (element uit #\orange Y=\orange{\mathbb{R}}# ) er in elke leeftijdscategorie zitten (element uit #\blue X# ). Het histogram is de bijbehorende grafiek.

Bekijk de onderstaande grafiek van een functie #f#.

Geef de waarde van #f(1)#.

#f(1)=# #-2#

We lezen dit af uit de grafiek door op de horizontale as de waarde #1# te zoeken.
Daarvandaan tekenen we een verticale lijn richting de grafiek.
Vanaf het snijpunt van de verticale lijn met de grafiek tekenen we dan een horizontale lijn richting de #y#-as.
Op de #y#-as lezen we af welke waarde van #y# bij de waarde van #x# hoort.

We vinden dan dat bij #x=1# de waarde van #y# gelijk is aan #y=-2#.

Nieuw voorbeeld