Exponentiële en logaritmische groei: Exponentiële groei
 Exponentiële groei
Exponentiële groei
Als een waarde \(c\) elk tijdsinterval van vaste lengte met hetzelfde percentage verandert, dan wordt \(c\) in feite iedere keer vermenigvuldigd met dezelfde factor. We hebben dan te maken met een constant veelvoud van een exponentiële functie.
Exponentiële groei-functie
Een exponentiële groei-functie heeft functievoorschrift \[f(x) = c \cdot g^x\]
Hierbij is
- \(c\) de beginwaarde, dat wil zeggen: de functiewaarde voor \(x=0\),
- \(g\) de groeifactor of het grondtal,
- \(x\) het argument of de exponent
Een groei die met een exponentiële groei-functie beschreven kan worden, noemen we ook wel een exponentiële groei-model of kortweg exponentiële groei.
De exponentiële groei-functie is alleen gedefinieerd voor \(g \gt 0\).
Dit heeft invloed op het bereik van een exponentiële groei-functie:
- Als \(c \gt 0\) dan \(f(x) \gt 0\) voor alle \(x\)
- Als \(c \lt 0\) dan \(f(x) \lt 0\) voor alle \(x\)
Hierin is \(y=0\) een horizontale asymptoot als \(g \neq 1\). Dit betekent dat de functie nooit de waarde #0# aanneemt, maar dat we functiewaarden er wel willekeurig dicht bij kunnen komen. De functiewaarde komt dichter en dichter bij #0# als #x# verder en verder van #0# komt. In het geval #g\gt 1#, nadert de functiewaarde #0# als #x# steeds verder van #0# weggaat in de negatieve richting. In het geval #0<g<1#, nadert de functiewaarde #0# als #x# steeds verder van #0# weggaat in de positieve richting.
- Als \(c = 0\), dan is #f(x)# de constante functie #0#, dat wil zeggen: \(f(x) = 0\) voor alle \(x\)
Om de kenmerken van een exponentiële groei-functie te kunnen bespreken voeren we twee begrippen in die op een willekeurige functie van toepassing zijn.
Groei en relatieve groei
Laat #a# en #p# getallen zijn met #p\ge0# en laat #f(x)# een functie zijn die gedefinieerd is voor alle #x# met #a\le x\le a+ p#.
- De waarde #f(a+p)-f(a)# heet de groei van #f(x)# tussen #a# en #a+p#.
- Als #f(a)\ne0# dan heet de waarde #\frac{f(a+p)-f(a)}{f(a)}# de relatieve groei van #f(x)# tussen #a# en #a+p#.
Hieronder geven we enkele kenmerkende eigenschappen van exponentiële groei.
Relatieve groei van het exponentiële groei-model
Laat #g# een positief getal zijn en #c# een constante ongelijk aan #0#.
- Als \(f(x) = c\cdot g^x\), dan is de relatieve groei van #f(x)# tussen elk tweetal punten #a# en #a+p# gelijk aan \[g^p-1\]
- De relatieve groei van een exponentiële groei-functie is onafhankelijk van de waarde van \(a\).
- De relatieve groei van een exponentiële groei-functie is onafhankelijk van de beginwaarde \(c\).
Als \(y = c\cdot g^x\), dan volgt uit de definitie dat de relatieve groei van het exponentiële groei-model tussen \(a\) en \(a+1\) gelijk is aan \(g-1\). We geven deze speciale waarde een eigen naam:
Groeivoet
De groeivoet van een exponentiële groei met functievoorschrift \(f(x) = c \cdot g^x\) is gelijk aan \(g-1\).
Als we de groeivoet met \(100\)% vermenigvuldigen, dan krijgen we de vaste procentuele toe- of afname van het exponentiële groei-model.
Zoals we bij de definitie van exponentiële groei-functie gezien hebben, hangt het van de grootte van #g# af of sprake is van toe- of afname.
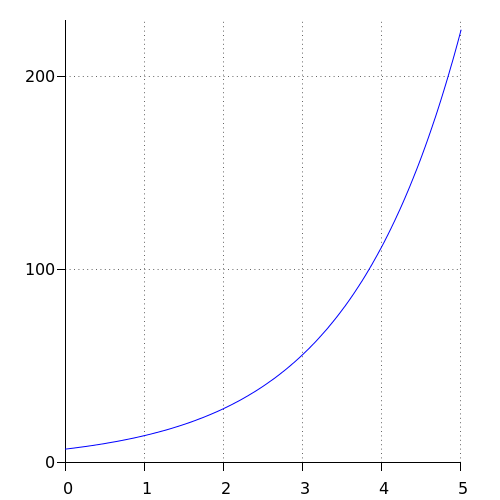
Voor een exponentiële groei met beginwaarde \(7\) en groeifactor \(2\) geldt \(y = 7\cdot 2^{x}\).
Als \(x\) toeneemt van \(3\) naar \(4\), dan neemt \(y\) toe van \(56\) naar \(112\). De groei van \(y\) op het interval #\ivcc{3}{4}# is dus \({112-56} = 56\).
De relatieve groei van \(y\) bij deze toename van \(x\) is dus \(\frac{112-56}{56} =\frac{56}{56} = 1\).
Maar ook bij elke andere toename met \(1\) voor \(x\) is de relatieve groei van \(y\) gelijk aan \( {1} \). De groeivoet van dit groeimodel is immers gelijk aan \( {2}-1 = {1} \).
De vaste procentuele toename van dit groeimodel is \(1 \cdot 100 = 100\)%.

omptest.org als je een OMPT examen moet maken.



