Lineaire lening

Rijen en reeksen: Financiële toepassingen van rijen en reeksen

Lineaire lening

Hier bespreken we de lineaire lening. We gebruiken dezelfde notatie als voor de bulletlening. In het bijzonder is #K# het geleende kapitaal, geeft #a_j# de aflossing in periode #j# aan en #r_j# de rentebetaling in die periode. De looptijd bedraagt #n# periodes. De grootte van de rentebetaling wordt bepaald door de groeivoet #i#.

Lineaire lening

Bij een lineaire lening worden de aflossingen gelijkmatig verdeeld over de totale looptijd. Aan het einde van elke periode wordt er een vast deel van de totaalschuld afgelost.

De lening wordt dus gekenmerkt door de volgende formules.

\[\begin{array}{rcl}\text{Aflossingen}&&a_{j} =\dfrac{K}{n}\\ \text{Rentebetalingen}&& r_j=\dfrac{n-j+1}{n} \cdot K \cdot i\\ \text{Schuldrest}&&R_j =\dfrac{n-j}{n} \cdot K\\ \end{array}\]

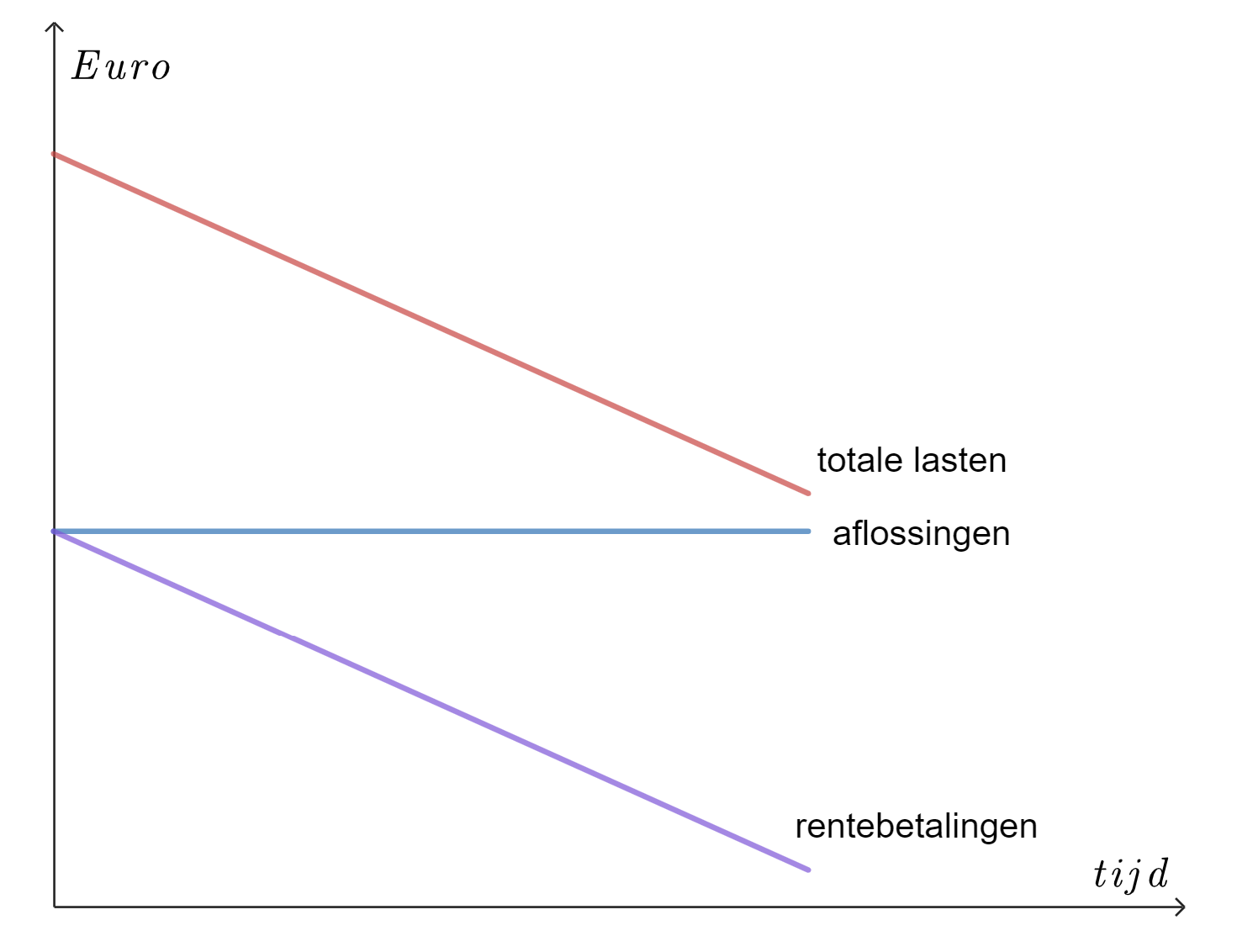
Doordat de nog openstaande schuld steeds kleiner wordt, hoeft er elke periode minder rente betaald te worden dan de periode ervoor. De lasten van een lineaire lening zijn relatief hoog aan het begin van de looptijd. maar deze worden steeds lager naarmate de tijd verstrijkt.

#r_1 \gt r_2 \gt r_3 \cdots \gt r_n#

Een 10%-lineaire lening van €100,000 met een looptijd van 10 jaar leidt tot onderstaande aflossingstabel.

Periode	Schuld begin	Rentebetaling	Aflossing	Schuld eind
#j#	#R_{j-1}#	#r_j#	#a_j#	#R_j#
1	100,000	10,000	10,000	90,000
2	90,000	9,000	10,000	80,000
3	80,000	8,000	10,000	70,000
4	70,000	7,000	10,000	60,000
5	60,000	6,000	10,000	50,000
6	50,000	5,000	10,000	40,000
7	40,000	4,000	10,000	30,000
8	30,000	3,000	10,000	20,000
9	20,000	2,000	10,000	10,000
10	10,000	1,000	10,000	0

In grafiek:

In periode #j# wordt hetzelfde bedrag afgelost als in alle andere periodes. Omdat er #n# periodes zijn en aan het eind de totale schuld #K# moet zijn afgelost, geldt #n\cdot a_j = K#, zodat #a_j = \dfrac{K}{n}#.

Aan het einde van periode #j# maar voor de afrekening over die periode, is er #j-1# keer afgelost. De restschuld bedraagt dan \[R_{j-1} = K-(j-1)\cdot a_j = K - (j-1)\cdot \dfrac{K}{n} = \frac{n-j+1}{n}\cdot K\] Daarover wordt aan het einde van de #j#-de periode \[r_j = R_{j-1}\cdot i = \frac{n-j+1}{n}\cdot K\cdot i\] aan rente betaald. De restschuld na betaling is \[R_j = K-j\cdot a_j = \frac{n-j}{n}\cdot K\]

Hiermee zijn de formules voor de lineaire lening afgeleid.

Gegeven is een 3%-lineaire lening van #\euro\,##120000# met een looptijd van #13# jaar.

Bereken de rentebetaling in jaar #9#, afgerond op twee decimalen.

#r_{9} =# #1384.62#

Gegeven:

kapitaal: #K = 120000#
interest: #i = 0.03#
looptijd: #n = 13#
periode: #j = 9#

Om de rentebetaling in periode #9# te berekenen maken we gebruik van de volgende formule:
\[\begin{array}{rcl}
r_j &=& \dfrac{n-(j-1)}{n}\cdot K\cdot i\\
&&\phantom{xxxxx}\color{blue}{\text{formule rentebetaling lineaire lening}}\\
r_{9} &=& \dfrac{13-(9-1)}{13}\cdot 120000\cdot 0.03\\
&&\phantom{xxxxx}\color{blue}{\text{waarden voor }n, j, K\text{ en }i\text{ ingevuld}}\\
&=& 1384.62\\
&&\phantom{xxxxx}\color{blue}{\text{uitgerekend}}\\
\end{array}\]

Nieuw voorbeeld