Introduction to differentiation: Definition of differentiation
The notion of difference quotient
In order to calculate the slope of a tangent line to a graph, we can take a line that lies close to the tangent line. For this line, you can calculate the slope by using the difference quotient.
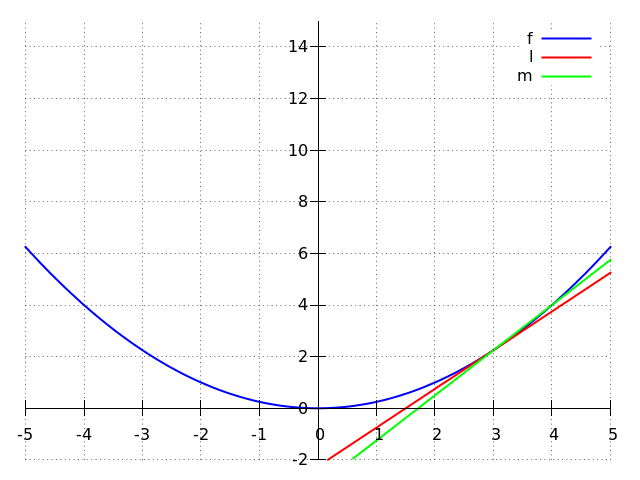
Approximate the slope of the tangent line #l# by calculating the slope of line #m#.
The slope of line #m# is given by:\[\begin{array}{rcl}\frac{\text{the difference in }y}{\text{the difference in }x}&=&\frac{\Delta y}{\Delta x}\\ &&\phantom{x}\color{blue}{\Delta y =\text{the difference between the }y\text{ coordinates}}\\
&&\phantom{x}\color{blue}{\text{of }\rv{3, {{19}\over{2}}}\text{ and }\rv{2, 7}}\\
&&\phantom{x}\color{blue}{\Delta x =\text{the difference between the }x\text{ coordinates}}\\
&&\phantom{x}\color{blue}{\text{of the same points}}\\
&=&\frac{{{19}\over{2}}-7}{3-2}\\ &=&{{5}\over{2}}\end{array}\]
We can therefore approximate the slope of the tangent line #l# by #3#.
As we will see later in this chapter, the actual slope of #l# is #2#.
Such an approximation of the slope of a tangent line of a graph is called a difference quotient. This is so called because it is actually the quotient of two differences #\Delta y# and #\Delta x# that express the change, #\Delta x# in #x# and the change, #\Delta y# in #y#, respectively.
Below the formal definition of the difference quotient is stated for the case where the graph is derived from a function.
The difference quotient
The difference quotient of a function #f# at #a# with difference #h# is
\[\frac{f (a+h)− f (a)}{h}\tiny.\]
The difference quotient measures the growth of #f# in the transition from #a# to #a+h#, normalized by the length #h# of the interval.
The illustration below shows the difference quotient of #f# at #a# with difference #h#.
As we see in the example and in the figure, the following rule applies:
Difference quotient and slope
The difference quotient of #f# at #a# with difference #h# is equal to the slope of the line through the points #\rv{a+h,f(a+h)}# and #\rv{a,f(a)}#.
A motivating example is the linear function #f(x)=c\cdot x+d#. The difference quotient of this function at #a# with difference #h# is \[\begin{array}{rcl}\frac{f(a+h)−f(a)}{h} &=&\frac{c\cdot(a+h)+d-(c\cdot a+d)}{h}\\&=&\frac{c\cdot a+c\cdot h+d-c\cdot a-d}{h}\\&=&\frac{c\cdot h}{h}\\&=&c\end{array}\]This is indeed the slope of the line #y=c\cdot x+d# through #\rv{a,f(a)}# and #\rv{a+h,f(a+h)}#.
Or visit omptest.org if jou are taking an OMPT exam.
