Inleiding tot differentiëren: Definitie afgeleide
Het begrip differentiequotiënt
Om de helling van een raaklijn aan een grafiek te berekenen kunnen we een lijn nemen die dichtbij de raaklijn ligt. Van deze lijn kun je de helling berekenen met behulp van het differentiequotiënt.
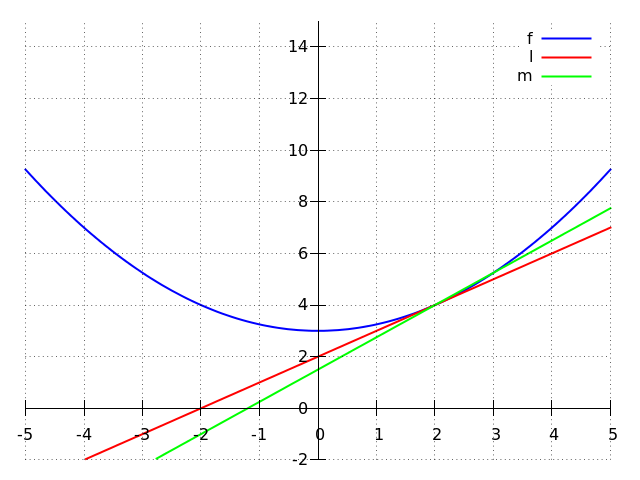
Benader de helling van de raaklijn #l# door de helling van lijn #m# te berekenen.
De helling van lijn #m# wordt gegeven door:\[\begin{array}{rcl}\dfrac{\text{het verschil in }y}{\text{het verschil in }x}&=&\dfrac{\Delta y}{\Delta x}\\ &&\phantom{x}\color{blue}{\Delta y =\text{het verschil tussen de }y\text{-coördinaten}}\\
&&\phantom{x}\color{blue}{\text{van }\rv{2, 7}\text{ en }\rv{1, {{11}\over{2}}}}\\
&&\phantom{x}\color{blue}{\Delta x =\text{het verschil tussen de }x\text{-coördinaten}}\\
&&\phantom{x}\color{blue}{\text{van dezelfde punten}}\\
&=&\dfrac{7-{{11}\over{2}}}{2-1}\\ &=&\displaystyle {{3}\over{2}}\end{array}\]
We kunnen de helling van de raaklijn dus benaderen door #2#.
Zoals we later in dit hoofdstuk zullen zien is de helling van #l# gelijk aan #1#.
Zo'n benadering van de helling van een raaklijn van een grafiek wordt een differentiequotiënt genoemd. Dit wordt zo genoemd, omdat het eigenlijk het quotiënt van twee verschillen (met een moeilijk woord: differentie) #\Delta y# en #\Delta x# is, die respectievelijk de verandering, #\Delta x#, in #x# en de verandering, #\Delta y#, in #y# uitdrukken.
Hieronder staat de formele definitie van het differentiequotiënt in het geval dat de grafiek van een functie afkomstig is.
Het differentiequotiënt
Het differentiequotiënt van een functie #f# in #a# met verschil #h# is
\[\frac{f (a+h)− f (a)}{h}\tiny.\]
Het differentiequotiënt meet de groei van #f# bij de overgang van #a# naar #a+h#, genormeerd naar de lengte #h# van het interval.
In de afbeelding hieronder is zichtbaar hoe het differentiequotiënt van #f# in #a# met verschil #h# eruitziet.
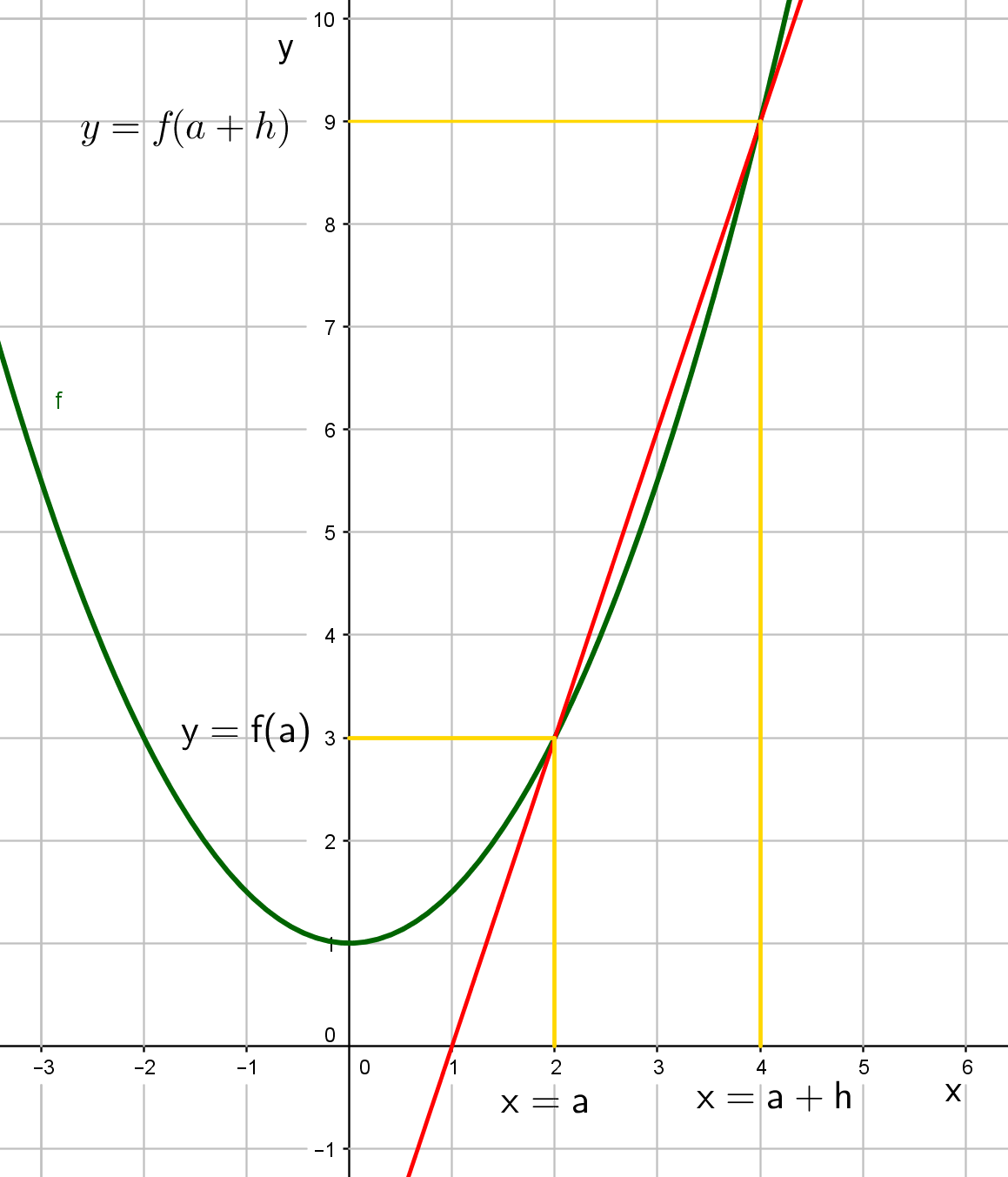
Zoals we in het voorbeeld en in de afbeelding zien geldt de volgende regel:
Differentiequotiënt en richtingscoëfficiënt
Het differentiequotiënt van #f# in #a# met verschil #h# is de richtingscoëfficiënt van de lijn door de punten #\rv{a+h,f(a+h)}# en #\rv{a,f(a)}#.
Een motiverend voorbeeld is de lineaire functie #f(x)=c\cdot x+d#. Het differentiequotiënt van deze functie in #a# met verschil #h# is\[\begin{array}{rcl}\frac{f(a+h)−f(a)}{h} &=&\frac{c\cdot(a+h)+d-(c\cdot a+d)}{h}\\&=&\frac{c\cdot a+c\cdot h+d-c\cdot a-d}{h}\\&=&\frac{c\cdot h}{h}\\&=&c\end{array}\]Dit is inderdaad de richtingscoëfficiënt van de lijn #y=c\cdot x+d# door #\rv{a,f(a)}# en #\rv{a+h,f(a+h)}#.
omptest.org als je een OMPT examen moet maken.
