Operations for functions: Inverse functions
 The notion of inverse function
The notion of inverse function
The inverse of an operation is an important notion in mathematics. For example for addition, the inverse is subtraction. And for multiplication it is division. The same can be applied to a real function. In the figure below, a real function #f# is shown, with domain #\{1,2,3\}# and range #\{2,4,8\}#. The function can be seen as an operation that maps the number #1# to #2#, the number #2# to #4#, and the number #3# to #8#.
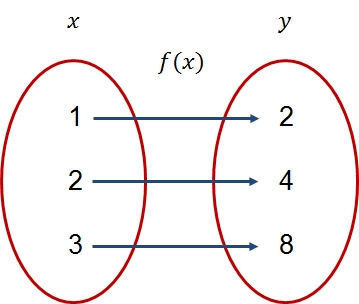
The inverse operation, in other words, the function that maps the number #2# to #1#, the number #4# to #2#, and the number #8# to #3# is called the inverse function: \(f^{-1}\). The function is shown in the following figure.
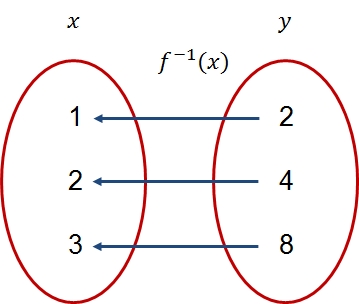
Inverse function
Let \(f\) and \(g\) be two functions such that the range of each of these is equal to the domain of the other. Consider the following two conditions:
- \(f(g(y))=y\) for each \(y\) in the domain of \(g\)
- \(g(f(x))=x\) for each \(x\) in the domain of \(f\)
If these two conditions are met, then the function \(g\) is said to be the inverse of the function \(f\) and \(f\) is said to be the inverse of \(g\). The inverse of #f# is also a function; it is denoted by \(f^{-1}\) and pronounced as \(f\)-inverse.
The inverse function #f^{-1}# of #f# satisfies \(f^{-1}(f(x))=x\) and \(f(f^{-1}(y))=y\) for all #x# in the domain of #f# and all #y# in the range of #f#.
Not every function is the inverse of a function. For instance, the function \(f\) with domain #\mathbb{R}# defined by the rule #f(x)=x^2# has no inverse. For, if #g# were to be its inverse, it would have to satisfy #g(x^2)=x#, for each #x\in\mathbb{R}#. But for #x=-1# and for #x=1# the left hand sides are the same and the right hand signs are each other's negatives: #-1=g((-1)^2)=g(1)=1#, a contradiction. Hence, \(f\) has no inverse nor is it the inverse of another function.
However, if we restrict the domain of the function \(f\) to the non-negative real numbers #\mathbb{R}_{\ge0}# (and keep the same function rule), then the function #g(x)=\sqrt{x}# is its inverse.
We will soon learn the requirements for a function to have an inverse.
We call it "the" inverse, because there can be no more than one inverse of a given function #f#: if #g# and #h# both satisfy the definition of the inverse of #f#, then:
\[\begin{array}{rcl} h(y) &=& h(f(g(y))\\ &&\phantom{xx}\color{blue}{y=f(g(y))}\\ &=& g(y)\\ &&\phantom{xx}\color{blue}{h(f(x))=x\text{ with } x=g(y)} \end{array}\]
so, indeed #h=g#.
The graph of a function #f# will be able to tell whether it has an inverse:
Calculation of the inverse function
Let #f# be a function.
Assume that #g# is a function whose range coincides with the domain of #f# and whose domain coincides with the range of #f#. The function #f# is the inverse of #g# if and only if at least one of the two equalities from the definition of invertibility holds.
Assume that #f# is an invertible function and that #x# belongs to the domain of #f#.
- The image #y=f(x)# of #x# satisfies #x=f^{-1}(y)#.
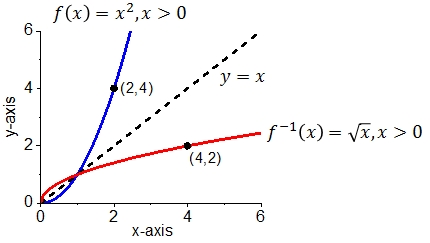
- The graph of #f^{-1}# can be obtained from the graph of #f# by reflecting it about the line with equation #y=x#.
Assume that, for #f# and #g#, the first equality of the definition of the inverse function holds: #f(g(y))=y# for all #y# in the domain of #g# (and hence, also the range of #f#). We prove the second equality of the definition. Let #x# be a point in the domain of #f#. Then #x# lies in the range of #g#, so there is a point #u# in the domain of #g# such that #x=g(u)#. Now we can rewrite #g(f(x))# in the following manner:
\[\begin{array}{rcl}g(f(x))&=& g(f((g(u)))=g(u)=x\end{array}\]With this we derived the second equality.
In the same way, the first equality can be derived from the second.
Now assume that #f# is invertible. We consider the two itemized statements.
If #y=f(x)#, then #x=f^{-1}(f(x)) =f^{-1}(y)#. This proves the first itemized statement.
Reflection about the line with equation #x=y# moves the point #\rv{x,f(x)}# from the graph of #f# to the point #\rv{f(x),x}=\rv{y,f^{-1}(y)}#: a point from the graph of #f^{-1}#. This proves the second itemized statement.
As an example, the graphs of the function #f(x)=x^2# with domain #\ivoo{0}{\infty}# and its inverse, the function #f^{-1}(x)=\sqrt{x}#, are drawn below.
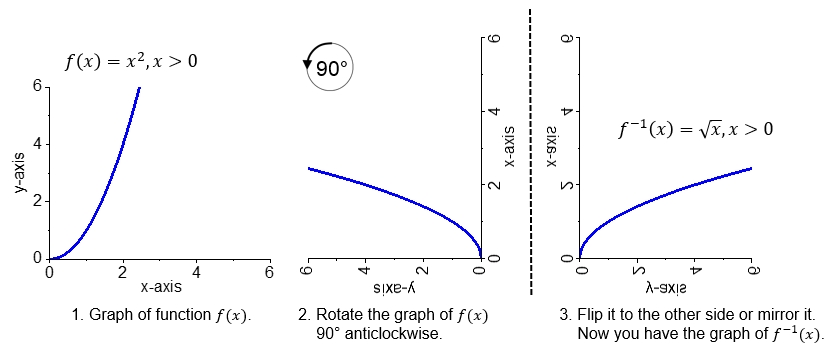
Another way to describe the graph of \(f^{-1}\) in terms of the graph of \(f\) is the following:
- draw the graph of \(f\) on a piece of transparent paper;
- turn the paper \(90^{\circ}\) counter clockwise (to the left);
- turn the paper over.
The graph thus constructed is the graph of #f^{-1}#. Here, the example #f(x)=x^2# is drawn again, this time with the steps just indicated for finding the inverse.
#f^{-1}(x)=# #x-7#
This is rather straightforward: the function #g# with function rule #g(x)=x-7# satisfies the two requirements for the inverse:
- #f(g(y))=f(y-7)=y-7+7=y#
- #g(f(x)) = g(x+7) = x+7-7 = x#
We explain how you can find this inverse function. For this purpose, we start with the equation #y=f(x)#, which we solve for #x#:
\[\begin{array}{rcl} y&=& x+ 7\\ &&\phantom{xx}\color{blue}{\text{the function rule}}\\ x + 7 &=& y\\
&&\phantom{xx}\color{blue}{\text{left and right hand side swapped}}\\ x&=& \displaystyle y- 7\\ &&\phantom{xx}\color{blue}{7\text{ subtracted left and right }}
\end{array}\]
In view of the Calculation of an inverse function we conclude that #f^{-1}(y)= y- 7#. The answer can be obtained by naming the argument #x# instead of #y#.

Or visit omptest.org if jou are taking an OMPT exam.



