Operations for functions: New functions from old
 Translating functions
Translating functions
We will consider various ways of manipulating a graph in the plane and study the consequences in case the graph is the graph of a function. We will begin by shifting the graph up or down.
Vertical translation
Let #a# be a real number. The vertical translation by #a# sends the point #\rv{x,y}# of the plane to #\rv{x,y+a}#.
Let \(f\) be a real function. Under the vertical translation by #a#, the graph of #f# is turned into the graph of the function of #x# with rule #f(x)+a#.
The graph of the function \(f\) moves upwards if \(a\gt0\) and downwards if \(a\gt0\).
The location of the zeros of the function \(f\) will change but the location of the minima and/or maxima will not change in terms of \(x\) but only in terms of \(y\) where \(a\) has to be added to the original value.
By way of example we have drawn two vertical translations of the graph of #f(x)=x^2-1#:
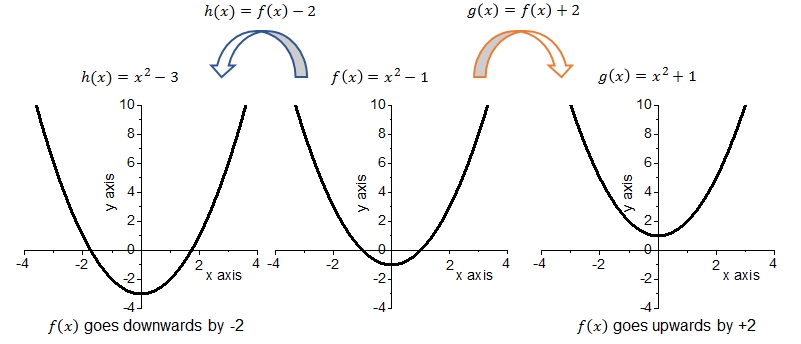
The following facts can be observed from these graphs:
- The graph of \(f\) is a parabola with zeros \(x=-1\) and \(x=1\) and a minimum at \(f(0)=-1\).
- The graph of \(h\) is a parabola with zeros \(x=\sqrt{3}\) and \(x=-\sqrt{3}\) and a minimum at \(f(0)=-3\).
- The graph of \(g\) is a parabola with no zeros and a minimum at \(f(0)=1\).
Next we deal with shifts of the graph to the left or right.
Horizontal translation
Let #a# a real number. The horizontal translation by #a# sends the point #\rv{x,y}# of the plane to #\rv{x+a,y}#.
Let \(f\) be a real function. Under the horizontal translation by #a#, the graph of #f# is turned into the graph of the function of #x# with rule #f(x-a)#.
The function \(f\) moves to the left if \(a\gt0\) and to the right if \(a\lt0\). The location of the zeros of the function \(f\) will move in the same direction (by adding \(a\) to the value of \(x\)) but the location of the minima and/or maxima will change in terms of \(x\) where \(a\) has to be added to the original value but the \(y\) will remain the same. By way of example we have drawn two vertical translations of the graph of #f(x)=x^2-1#:
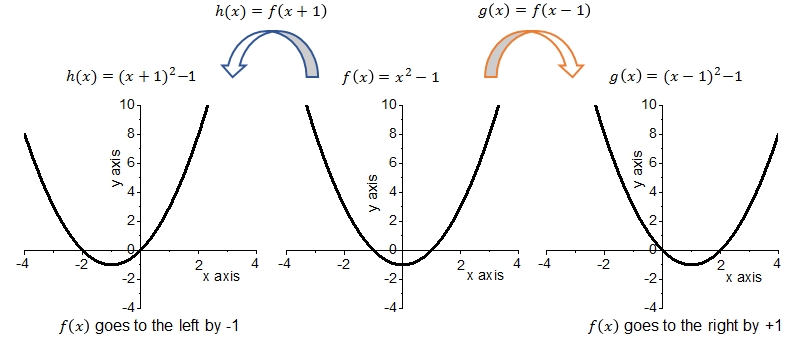
The following facts can be observed from these graphs:
- The graph of \(f\) is a parabola with zeros \(x=-1\) and \(x=1\) and a minimum at \(f(0)=-1\).
- The graph of \(h\) is a parabola with zeros \(x=-2\) and \(x=0\) and a minimum at \(f(-1)=-1\).
- The graph of \(g\) is a parabola with zeros \(x=0\) and \(x=2\) and a minimum at \(f(1)=-1\).
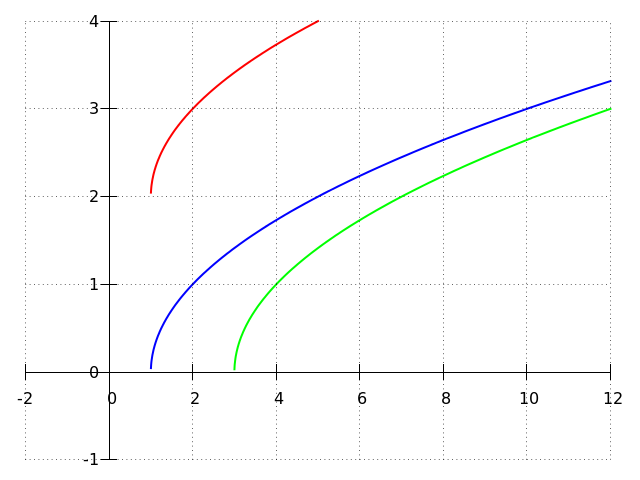
The vertical translation of the graph belongs to the function #2+ f(x) = 2 + \left(\sqrt{x-1}\right)# is red.
The horizontal translation of the graph belongs to the function # f\left({x- 2}\right) = \sqrt{x-3}# is green.

Or visit omptest.org if jou are taking an OMPT exam.