The graph of #f# consists of all points of the form #\rv{x,f(x)}#. Under scaling by #a#, these points become #\rv{x,a\cdot f(x)}# which are indeed the points of the graph of the function #a\cdot f#.

The points of the plane stretched vertically if \(a\gt0\) and shrunk vertically if \(a\lt0\). In the case \(a\lt0\) the graph will also flip about the #x#-axis (the originated graph will be the mirror reflection of \(f\) about the \(x\) axis). The location of the zeros of the function \(f\) will be the same as well as the location of the minimums and/or maximums that will only change in terms of \(y\) by the factor \(a\).

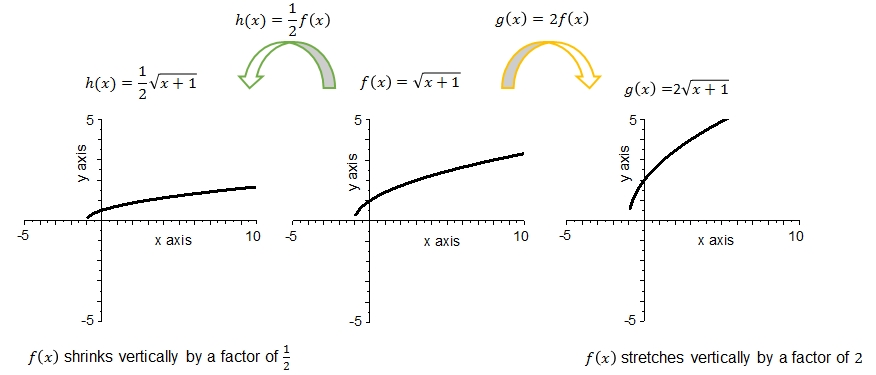
The following facts can be observed in the above graphs:

• The graph of \(f\) is the square root of \(\sqrt{x+1}\) with zero \(x=-1\) and a minimum at \(f(-1)=0\).
• The graph of \(h\) is the square root of \(\sqrt{x+1}\) multiplied by \(\frac{1}{2}\) with zero \(x=-1\) and a minimum at \(f(-1)=0\).
• The graph of \(g\) is the square root of \(\sqrt{x+1}\) multiplied by \(2\) with zero \(x=-1\) and a minimum at \(f(-1)=0\).

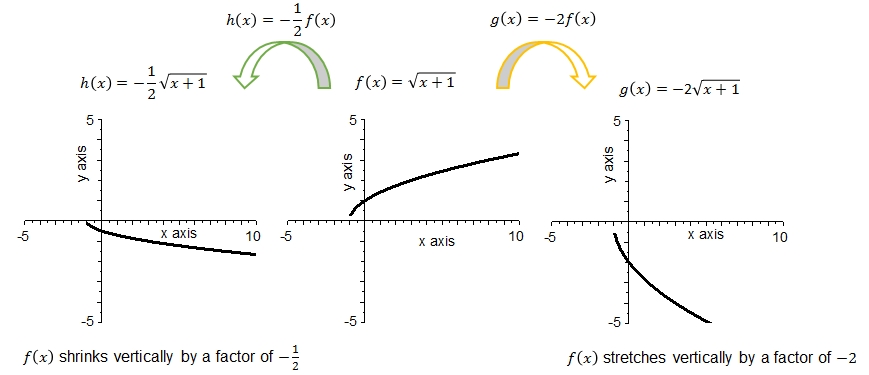
The following facts can be observed in the above graphs:

• The graph of \(f\) is the square root of \(\sqrt{x+1}\) with zero \(x=-1\) and a minimum at \(f(-1)=0\).
• The graph of \(h\) is the square root of \(\sqrt{x+1}\) multiplied by \(-\frac{1}{2}\) with zero \(x=-1\) and a maximum at \(f(-1)=0\).
• The graph of \(g\) is the square root of \(\sqrt{x+1}\) multiplied by \(-2\) with zero \(x=-1\) and a maximum at \(f(-1)=0\).

Putting #x_1=a\cdot x#, we have #\rv{a\cdot x,f(x)}=\rv{x_1,f\left(\frac{x_1}{a}\right)}#. This shows that the function rule of the function whose graph is obtained by the horizontal scaling of the graph of #f#, is equal to #f\left(\frac{x_1}{a}\right)#.

The function \(f\) is shrunk horizontally if \(a\gt1\) or \(a\lt-1\) by a factor of \(\frac{1}{a}\) and stretched horizontally if \(-1\lt a\lt 1\) by a factor of \(a\) with \(a\neq 0\).

In case \(a\lt0\), the graph will also flip about the #y#-axis (the originated graph will be the mirror reflection of \(f\) about the \(y\)-axis). The location of the zeros of the function \(f\) as well as the location of the minima and/or maxima will change, whereas in terms of \(y\) the minima and/or maxima will remain the same.

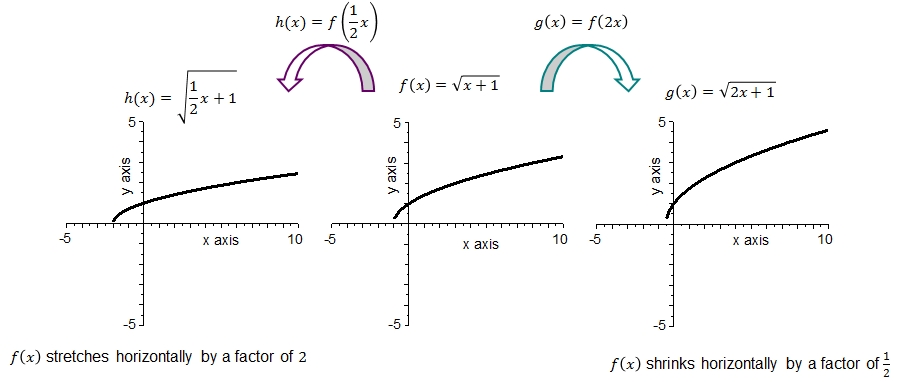
It is possible to observe the following facts from the above graphs:

• The graph of \(f\) is the square root of \(\sqrt{x+1}\) with zero \(x=-1\) and a minimum at \(f(-1)=0\).
• The graph of \(h\) is the square root of \(\sqrt{\frac{1}{2}x+1}\) with zero \(x=-2\) and a minimum at \(f(-2)=0\).
• The graph of \(g\) is the square root of \(2x+1\) with zero \(x=-\frac{1}{2}\) and a minimum at \(f(-\frac{1}{2})=0\).

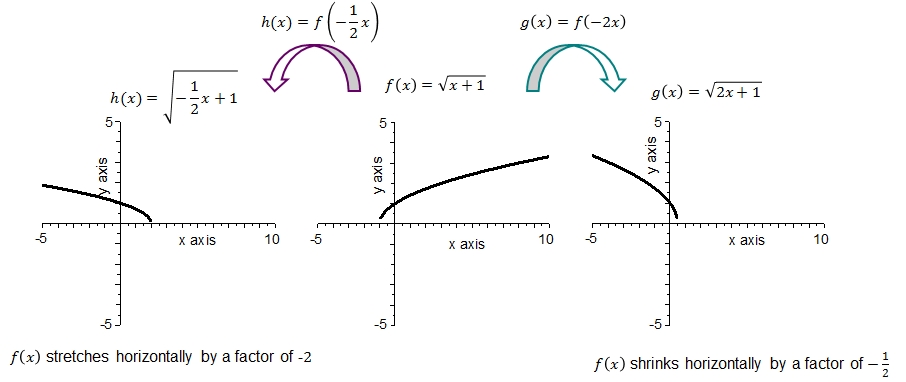
It is possible to observe the following facts from the above graphs:

• The graph of \(f\) is the square root of \(\sqrt{x+1}\) with zero \(x=-1\) and a minimum at \(f(-1)=0\).
• The graph of \(h\) is the square root of \(-\sqrt{\frac{1}{2}x+1}\) with zero \(x=2\) and a minimum at \(f(2)=0\).
• The graph of \(g\) is the square root of \(-2x+1\) with zero \(x=\frac{1}{2}\) and a minimum at \(f(\frac{1}{2})=0\).