Schalen van functies

Bewerkingen met functies: Nieuwe functies uit oude

Schalen van functies

We gaan nu het vergroten of verkleinen van een grafiek in horizontale of verticale richting bestuderen.

Verticale verschalen

Laat #a# een reëel getal zijn, ongelijk aan #0#. Verticaal verschalen met #a# verplaatst het punt #\rv{x,y}# in het vlak naar #\rv{x,a\cdot y}#.

Onder verticale verschaling met #a# wordt de grafiek van een functie #f# omgezet in de grafiek van #a\cdot f#, dat wil zeggen: de functie van #x# met functievoorschrift #a\cdot f(x)#.

De grafiek van #f# bestaat uit alle punten van de vorm #\rv{x,f(x)}#. Door verschaling met #a# worden deze punten omgezet naar #\rv{x,a\cdot f(x)}#, die inderdaad behoren tot de grafiek van de functie #a\cdot f#.

De punten van het vlak worden verticaal uitgerekt als \(a\gt0\) en krimpen verticaal als \(a\lt0\). In het geval \(a\lt0\) zal de grafiek ook gespiegeld worden in de #x#-as (de ontstane grafiek zal de weerspiegeling zijn van \(f\) in de \(x\)-as). De ligging van de nulpunten van de functie \(f\) zullen dezelfde zijn als de locatie van de minima en/of maxima die alleen zal veranderen in termen van \(y\) met de factor \(a\).

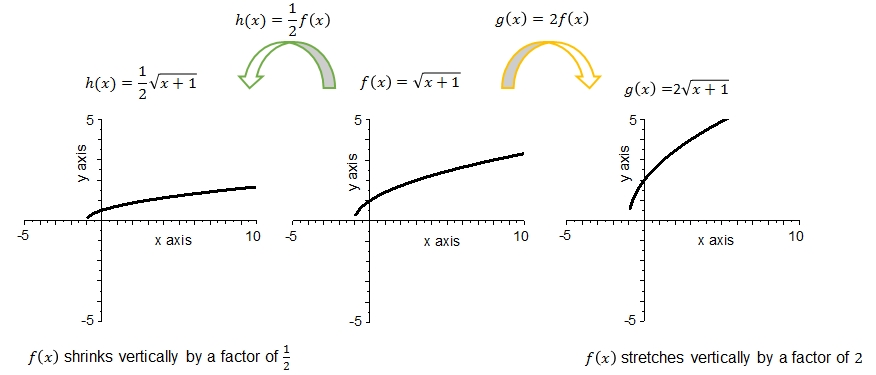
De volgende gegevens kunnen worden waargenomen in de bovenstaande grafieken:

De grafiek van \(f\) is de vierkantswortel van \(\sqrt{x+1}\) met nulpunt \(x=-1\) en een minimum bij \(f(-1)=0\).
De grafiek van \(h\) is de vierkantswortel van \(\sqrt{x+1}\) vermenigvuldigd met \(\frac{1}{2}\) met nulpunt \(x=-1\) en een minimum bij \(f(-1)=0\).
De grafiek van \(g\) is de vierkantswortel van \(\sqrt{x+1}\) vermenigvuldigd met \(2\) met nulpunt \(x=-1\) en een minimum bij \(f(-1)=0\).

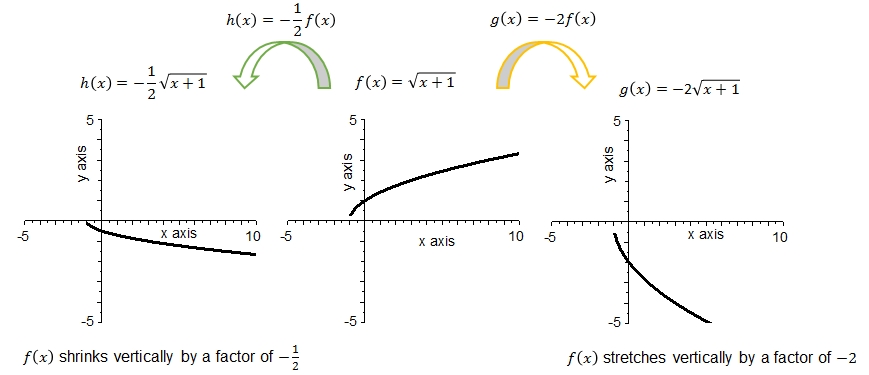
De volgende gegevens kunnen worden waargenomen in de bovenstaande grafieken:

De grafiek van \(f\) is de vierkantswortel van \(\sqrt{x+1}\) met nulpunt \(x=-1\) en een minimum bij \(f(-1)=0\).
De grafiek van \(h\) is de vierkantswortel van \(\sqrt{x+1}\) vermenigvuldigd met \(-\frac{1}{2}\) met nulpunt \(x=-1\) en een maximum bij \(f(-1)=0\).
De grafiek van \(g\) is de vierkantswortel van \(\sqrt{x+1}\) vermenigvuldigd met \(-2\) met nulpunt \(x=-1\) en een maximum bij \(f(-1)=0\).

Horizontaal verschalen

Laat #a# een reëel getal zijn, ongelijk aan #0#. Horizontaal verschalen met #a# verplaatst het punt #\rv{x,y}# van het vlak naar #\rv{a\cdot x,y}#.

Onder horizontale verschaling met #a# wordt de grafiek van een functie #f# omgezet in de grafiek van de functie met functievoorschrift # f\left(\frac{x}{a}\right)#.

Als we stellen dat #x_1=a\cdot x#, hebben we #\rv{a\cdot x,f(x)}=\rv{x_1,f\left(\frac{x_1}{a}\right)}#. Dit toont aan dat het functievoorschrift van de functie waarvan de grafiek wordt verkregen door de horizontale verschaling van de grafiek van #f# gelijk is aan #f\left(\frac{x_1}{a}\right)#.

De functie \(f\) is horizontaal gekrompen met een factor \(\frac{1}{a}\) als \(a\gt1\) of \(a\lt-1\) en horizontaal uitgerekt met een factor \(a\) met \(a\neq 0\) als \(-1\lt a\lt 1\).

In het geval \(a\lt0\), zal de grafiek ook flip om de #y#-as spiegelen (de ontstane grafiek zal weerspiegeling zijn van \(f\) in de \(y\)-as). De ligging van de nulpunten van de functie \(f\) en de locatie van de minima en/of maxima veranderen, terwijl de minima en/of maxima in termen van \(y\) hetzelfde blijven.

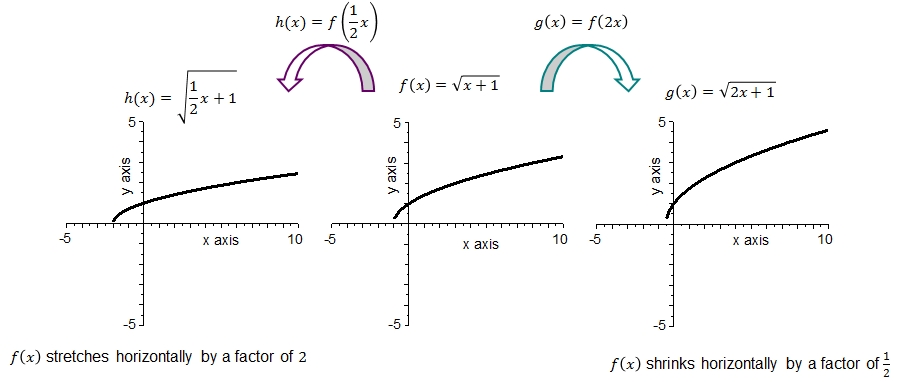
Het is mogelijk om de volgende feiten waar te nemen uit de bovenstaande grafieken:

De grafiek van \(f\) is de vierkantswortel van \(\sqrt{x+1}\) met nulpunt \(x=-1\) en een minimum bij \(f(-1)=0\).
De grafiek van \(h\) is de vierkantswortel van \(\sqrt{\frac{1}{2}x+1}\) met nulpunt \(x=-2\) en een minimum bij \(f(-2)=0\).
De grafiek van \(g\) is de vierkantswortel van \(2x+1\) met nulpunt \(x=-\frac{1}{2}\) en een minimum bij \(f(-\frac{1}{2})=0\).

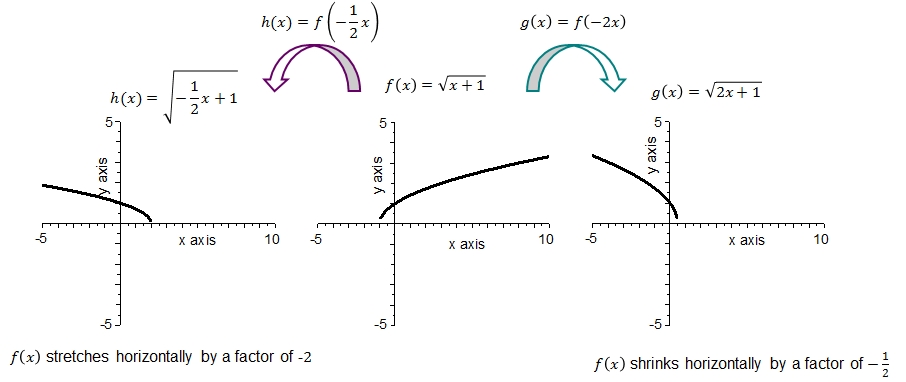
Het is mogelijk om de volgende feiten waar te nemen uit de bovenstaande grafieken:

De grafiek van \(f\) is de vierkantswortel van \(\sqrt{x+1}\) met nulpunt \(x=-1\) en een minimum bij \(f(-1)=0\).
De grafiek van \(h\) is de vierkantswortel van \(-\sqrt{\frac{1}{2}x+1}\) met nulpunt \(x=2\) en een minimum bij \(f(2)=0\).
De grafiek van \(g\) is de vierkantswortel van \(-2x+1\) met nulpunt \(x=\frac{1}{2}\) en een minimum bij \(f(\frac{1}{2})=0\).

Neem aan dat #f(x)= \sqrt{x-4}#. Hieronder staan de grafieken van #f#, en de verticale en de horizontale verschaling met #3# getekend.

Welke grafiek hoort bij welke verschaling?

De grafiek van #f# is blauw.
De verticale verschaling van de grafiek hoort bij de functie #3\cdot f(x) = 3\cdot\left(\sqrt{x-4}\right)# #=3\cdot \sqrt{x-4}# en is rood.
De horizontale verschaling hoort bij de functie # f\left(\frac{x}{3}\right) = \sqrt{{{x}\over{3}}-4}# #={{\sqrt{x-12}}\over{\sqrt{3}}}# en is groen.

Nieuw voorbeeld