Functions: Quadratic functions
 Introduction
Introduction
A quadratic function #f# is given by #f(x)=ax^2+bx+c# with #a#, #b# and #c# being real numbers and #a\neq 0#.
The graph associated with such a function is called a parabola.
When #a\gt0# then we speak of a parabola opening upwards and when #a\lt0# of a parabola opening downwards.
The significance of these names becomes evident from the graph below of the parabola opening upwards of #x^2-8# and the parabola opening downwards of #-x^2+8#.
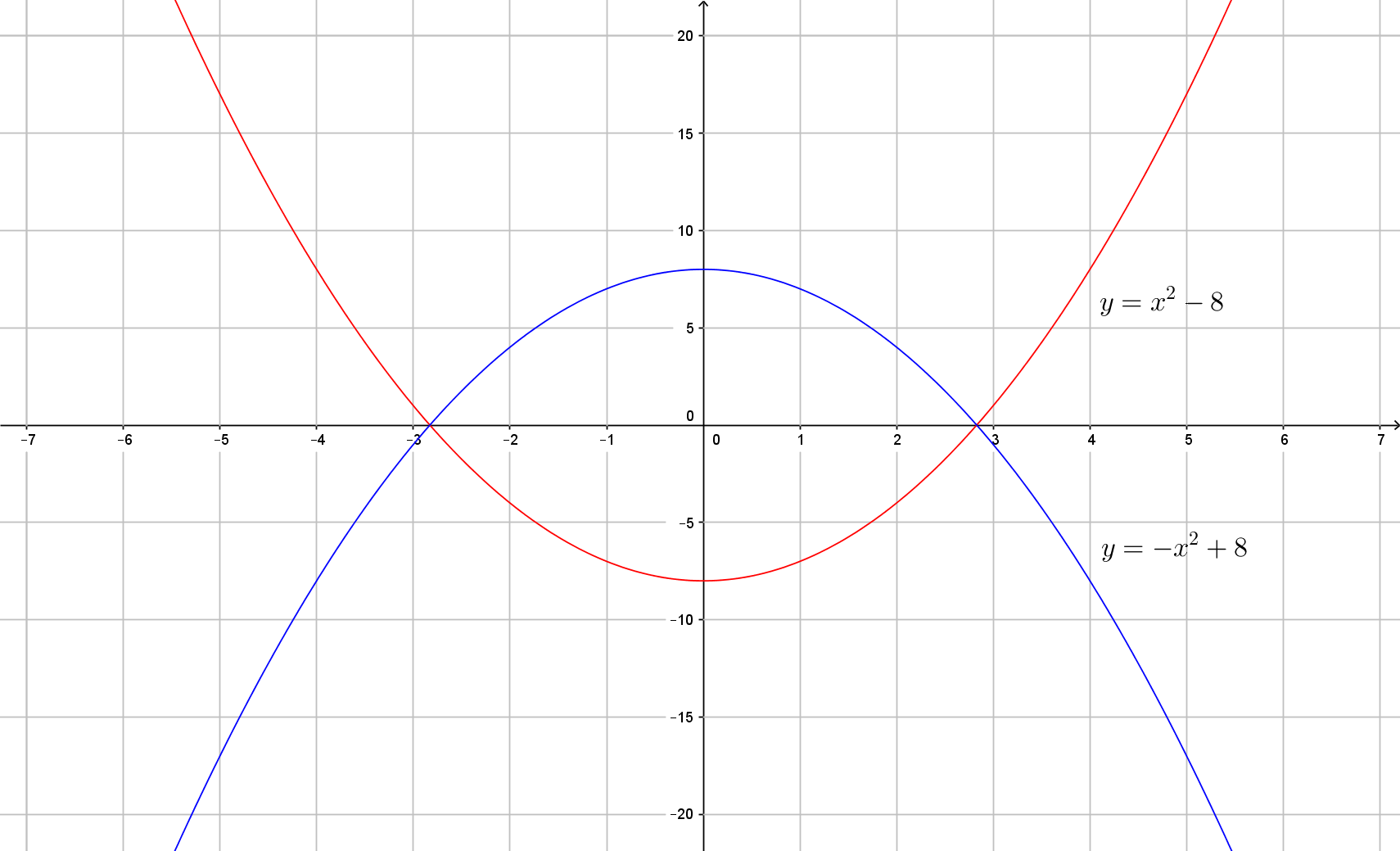
To find the zeros of a quadratic function, we need to find the points of intersection of the parabola with the #x#-axis. We can do this in three ways:
- completing the square
- #abc#-formula
- factorization
Unlock full access


Teacher access
Request a demo account. We will help you get started with our digital learning environment.
Student access
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.



