Functies: Inleiding tot functies
 Continuïteit
Continuïteit
Continuïteit
Laat #f# een reële functie zijn die gedefinieerd is op een open interval rond een punt #a#.
Als #\displaystyle \lim_{x\to a}f(x) =f(a)#, dan heet #f# continu in #a#. Zo niet, dan heet #f# discontinu in #a#.
Als #f# continu is in elk punt van een open interval #\ivoo{c}{d}#, dan heet #f# continu op #\ivoo{c}{d}#.
Anders gezegd, een functie is continu wanneer de grafiek getekend kan worden zonder je pen van het papier te halen.
Op het moment dat een functie #f(x)# niet gedefinieerd is in het punt #x#, dan bestaat de functie niet in dat punt en is de functie discontinu.
Wanneer de grafiek van een functie #f# een "sprong" vertoont, dan spreken we van een discontinue functie.
We laten een functie zien die bijna overal continu is, maar niet in het punt #0#. De functie is de Heaviside functie #H#, gedefinieerd door #H(x) = 0# als #x\lt0# en #H(x) = 1# als #x\gt0#. De grafiek van deze functie vertoont een sprong in #0# en is daar dus discontinu.

De functie #f# is linkscontinu in #x=1#:
\[
\begin{array}{rcl}
\displaystyle\lim_{x\uparrow1}f(x)&=&\lim_{x\uparrow1}( 7x+9)=7+9=16=f(1)\end{array}\]
De functie #f# is rechtscontinu in #x=1#:
\[\begin{array}{rcl}\displaystyle\lim_{x\downarrow1}f(x)&=&\lim_{x\downarrow1} (9 x^2+7)=9+7=16=f(1)\end{array}\]
Omdat #f# in #1# zowel links- als rechtscontinu is, concluderen we dat de functie continu is in #1#.
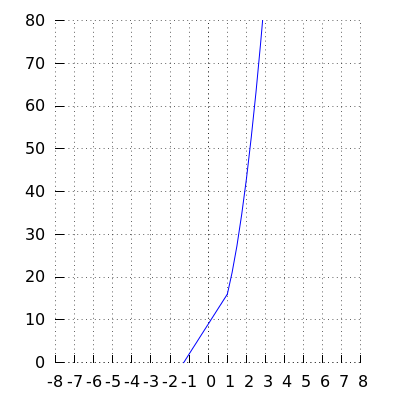
Hieronder staat de grafiek van #f#. De grafiek maakt geen sprong in #1#.

omptest.org als je een OMPT examen moet maken.



