Optimization: Extreme points
 Stationary points
Stationary points
The concepts of stationary point, minimum, and maximum are already known for functions of a single variable. The function \(f(x)\) has a local minimum in \(x=a\) if the graph near \(x=a\) lies above \(f(a)\), more precisely, if there are numbers #c\lt a# and #d\gt a# such that \(f(x)\ge f(a)\) for all \(x\) from \(\ivoo{c}{d}\). For a differentiable function \(f(x)\), a local minimum (or maximum) is a stationary point, that is, a point \(x=a\) at which the tangent line to \(f\) is horizontal, in other words \(f'(a)=0\).
As with functions of one variable we will examine local minima and maxima of bivariate functions. We start with the two-dimensional counterpart of the concept of stationary point.
Stationary point
Let #f# be a bivariate differentiable function. A point \(\rv{a,b}\) is a stationary point of the function \(f(x,y)\) if all partial derivatives of #f# at this point are equal to zero.
Stationary points can be found by solving the following system of equations: \[\eqs{f_x(x,y)&=&0\cr f_y(x,y)&=&0\cr}\]
Later we will see that, if #\rv{a,b}# is a stationary point of #f#, the tangent plane to the graph of #f# at \(\rv{a,b,f(a,b)}\) is horizontal.
The partial derivatives of #f# are \[f_x(x,y)=2\cdot y\cdot x+y^2-y\phantom{quad}\text{and}\phantom{quad}f_y(x,y)=x^2+2\cdot y\cdot x-x\tiny.\] The stationary points are the solutions of the system of equations \[\lineqs{2\cdot y\cdot x+y^2-y&=&0\cr x^2+2\cdot y\cdot x-x&=&0\cr}\] To solve this system, we split it into smaller systems by factoring the left members of the equations. We find: \[\lineqs{y\cdot \left(2\cdot x+y-1\right)&=&0\cr x\cdot \left(x+2\cdot y-1\right)&=&0\cr}\] Apparently, each of the equations can be split into two simpler equations. Combination of the four possibilities leads to four solutions:
- \(\eqs{x&=&0\cr y&=&0\cr}\phantom{xx} \implies\) \(\phantom{xx} \rv{x,y}=\rv{0,0}\)
- \(\eqs{ x+2\cdot y-1&=&0\cr y&=&0\cr} \phantom{xx} \implies\) \(\phantom{xx} \rv{x,y}=\rv{1,0}\)
- \(\eqs{ x&=&0\cr 2\cdot x+y-1&=&0\cr}\phantom{xx} \implies \) \(\phantom{xx} \rv{x,y}=\rv{0,1}\)
- \(\eqs{ 2\cdot x+y-1&=&0\cr x+2\cdot y-1&=&0\cr}\phantom{xx}\implies\) \(\phantom{xx} \rv{x,y}=\rv{{{1}\over{3}},{{1}\over{3}}}\)
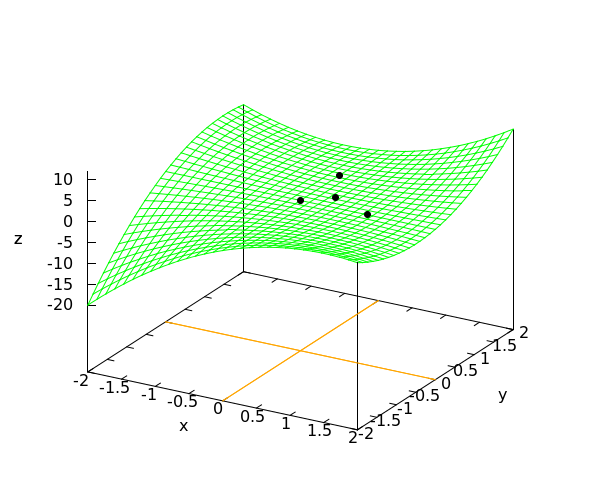
We conclude that there are four stationary points: #\left\{\rv{0,0},\rv{1,0},\rv{0,1}, \rv{{{1}\over{3}},{{1}\over{3}}}\right\}#.
The graph of the function #f# is shown in the figure below. The points of the graph associated with #\left\{\rv{0,0},\rv{1,0},\rv{0,1}, \rv{{{1}\over{3}},{{1}\over{3}}}\right\}# are marked with a small black disk.

Or visit omptest.org if jou are taking an OMPT exam.



