Optimization: Extreme points
 Minimum, maximum, and saddle point
Minimum, maximum, and saddle point
The concepts of local minimum and local maximum are already known to us for functions of a single variable. The function \(f(x)\) has a local minimum in \(x=a\) if the graph near \(x=a\) lies above \(f(a)\), more precisely, if there is an open interval \(\ivoo{c}{d}\) around \(a\) (that is to say, there are numbers #c\lt a# and #d\gt a#) such that \(f(x)\ge f(a)\) for all \(x\) from \(\ivoo{c}{d}\). For the definition in the case of a function of two variables, we replace the open interval by an open disk.
Local extremes
Let #\epsilon# be a positive number. The open disk around a point #p# of #{\mathbb R}^2# of radius #\epsilon# is the subset #S_{p,\epsilon}# of #{\mathbb R}^2# consisting of all points #q\in {\mathbb R}^2# at distance less than #\epsilon# to #p#. In a formula: \[S_{p,\epsilon}=\left\{q\in{\mathbb R}^2\mid \sqrt{(p_1-q_1)^2 + (p_2-q_2)^2}\lt \epsilon\right\}\]
Let #f# be a bivariate function with domain #D# and let #p# be a point of #D#.
- The point #p# is called a local minimum of #f# if there is an open disk #S# around #p# (a set of the form #S=S_{p,\epsilon}#) for a suitable value of #\epsilon# so #f(q)\ge f(p)# for all #q\in D\cap S#.
- The point #p# is called a local maximum of #f# if there is an open disk #S# around #p# so #f(q)\le f(p)# for all #q\in D\cap S#
- The point #p# is called a saddle point of #f# if it is a stationary point, but in every open disk around #p# there are points \(q\) and \(r\) such that \(f(q)\gt f(p)\) and \(f(r)\lt f(p)\).
Points #p# with #f(x)\le f(p)# for all #x# from the domain of #f# are called maxima. Points #p# with #f(x)\ge f(p)# for all #x# from the domain of #f# are called minima.
Clearly, a maximum of #f# will always be a local maximum and a minimum will always be a local minimum. In order to distinguish maxima and minima from local maxima and minima, we sometimes also call them global maxima and global minima.
Below you see the graph of the function \[f(x,y)=\tfrac{1}{2}\!\left((1-(x-\tfrac{1}{2})^2-(y-\tfrac{1}{2})^2\right)\]

This function has the following partial derivatives: \[f_x(x,y)=\tfrac{1}{2}-x\qquad\text{and}\qquad f_y(x,y)=\tfrac{1}{2}-y\] In the point \(\rv{\tfrac{1}{2},\tfrac{1}{2}}\), both derivatives are zero. This point is a stationary point. The function has a maximum value there.
The notion of saddle point is similar to the notion of inflection point for a stationary point of a function of a single variable.
Here is a generalization of the theorem Local extrema are stationary points for one variable.
If #f# a bivariate differentiable function on a domain #D# and #p# is a local minimum or local maximum of #f#, then #p# is a stationary point of #f#.
Since a local maximum of a multivariate differentiable function is a stationary point, we first calculate the stationary points. The partial derivatives of #f# are \[f_x(x,y)=-4\cdot x-2\cdot y+36\phantom{quad}\text{and}\phantom{quad}f_y(x,y)=-2\cdot x-4\cdot y+42\tiny.\] The stationary points are the solutions of the system of equations \[\lineqs{-4\cdot x-2\cdot y+36&=&0\cr -2\cdot x-4\cdot y+42&=&0\cr}\]
This system has exactly one solution: #{x = 5\land y = 8}#. We conclude that there is exactly one stationary point: #\rv{5, 8}#. It is given that #f# has a local maximum, so this point must be the answer: #\rv{5, 8}#.
The graph of the function #f# is shown in the figure below. The point #\rv{5,8,261}# corresponding to the local maximum is indicated by a small black disk.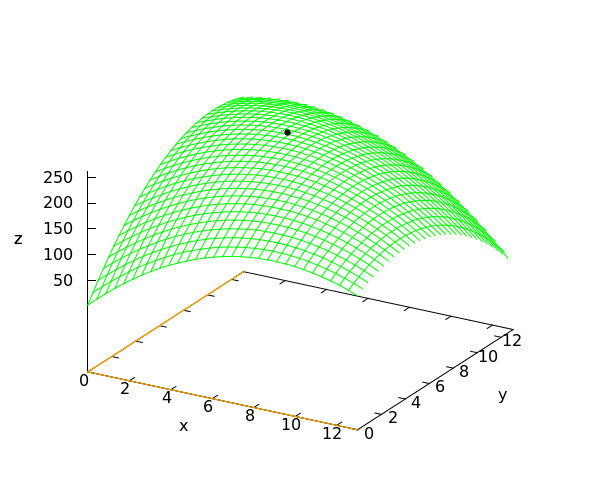

Or visit omptest.org if jou are taking an OMPT exam.




