Drawing of parabolas

Quadratic equations: Drawing parabolas

Drawing of parabolas

We have seen that the graph of a quadratic is a parabola. We have also seen how the intersection points with the axes, the vertex and other points with particular values of #x# of the parabola can be calculated. From these calculated values we can easily draw the graph of a quadratic.

Procedure drawing parabola

	Procedure	geogebra plaatje
	We will draw the graph of a quadratic.
Step 1	Determine the intersection point with the #y#-axis.
Step 2	Determine the vertex.
Step 3	Determine the intersection points with the #x#-axis, if there are any.
Step 4	Substitute values for #x# in the formula in such a way that we have at least 4 points we can draw.
Step 5	Draw these points in the coordinate system and connect them by a smooth parabola.

SymmetryWhen doing step 4, you can limit the number of points we need to calculate by using symmetry. A parabola is symmetrical, it is reflected in a vertical line through the vertex.

See the graph that belongs to the following formula:
\[y=x^2-x-5\]
Draw the intersection with the #y#-axis, the vertex, and the intersections with the #x#-axis.

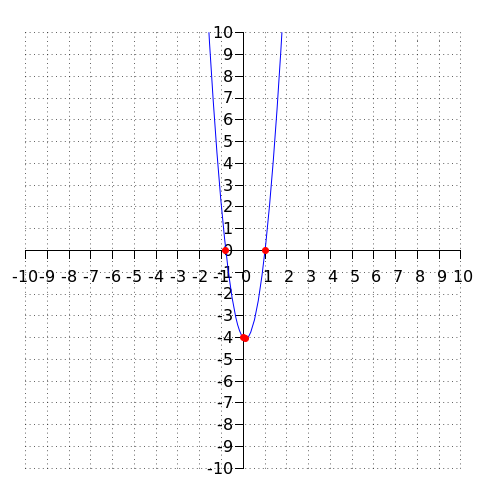
The red dots are the four dots from the question. These are calculated as followed:
The formula is already written in the form of #a \cdot x^2+b \cdot x +c# with #a =1#, #b=-1# and #c=-5#. Seeing as #a>0# the graph is a parabola that opens upward.

The intersection with the #y#-axis is equal to the value of the constant in the quadratic formula, which is equal to #-5#. That means that the coordinates of the intersection point with the #y#-axis are #\rv{0,-5}#.

The #x#-value of the vertex is given by #x=-\dfrac{b}{2 \cdot a}# and is equal to:
\[\begin{array}{rclrl}
x&=& -\dfrac{-1}{2 \cdot 1} &&\phantom{xxx}\color{blue}{\text{formula entered}}\\
&=& {{1}\over{2}} &&\phantom{xxx}\color{blue}{\text{simplified}}\\
\end{array}\]
The #y#-value of the vertex is calculated by entering #x={{1}\over{2}}# in the formula. Which gives:
\[\begin{array}{rclrl}
y&=& {{1}\over{2}}^2 -{{1}\over{2}} -5
&&\phantom{xxx}\color{blue}{\text{formula entered}}\\
&=& -{{21}\over{4}} &&\phantom{xxx}\color{blue}{\text{calculated}}\\
\end{array}\]
The coordinates of the vertex are: #\rv{{{1}\over{2}},-{{21}\over{4}}}#. To draw the point in the graph, we have to write the coordinates as decimal numbers (rounded to 1 decimal). That gives: #\rv{0.5,-5.2}#.

The intersections with the #x#-axis are the points that correspond to #y=0#.
\[\begin{array}{rcl}
x^2-x-5 &=& 0 \\&&\phantom{xxx}\color{blue}{\text{the equation that should be calculated}}\\
x=\dfrac{-{-1}-\sqrt{\left(-1\right)^2-4 \cdot 1 \cdot -5}}{2 \cdot 1} &\vee& x=\dfrac{-{-1}+\sqrt{\left(-1\right)^2-4 \cdot 1 \cdot -5}}{2 \cdot 1} \\&&\phantom{xxx}\color{blue}{\text{quadratic formula entered}}\\
x={{1-\sqrt{21}}\over{2}} &\vee& x={{\sqrt{21}+1}\over{2}} \\&&\phantom{xxx}\color{blue}{\text{calculated}}\\
\end{array}\]
The coordinates of the intersections with the #x#-axis are: #\rv{{{1-\sqrt{21}}\over{2}},0}# and #\rv{{{\sqrt{21}+1}\over{2}},0}#. To draw the point in the graph, we have to write the coordinates as decimal numbers (rounded to 1 decimal). That gives:#\rv{-1.8,0}# and #\rv{2.8,0}#.

The four points in the graph are: #\rv{0,-5}#, #\rv{{{1}\over{2}},-{{21}\over{4}}}#, #\rv{{{1-\sqrt{21}}\over{2}},0}# and #\rv{{{\sqrt{21}+1}\over{2}},0}#.

The formula is already written in the form of #a \cdot x^2+b \cdot x +c# with #a =1#, #b=-1#, and #c=-5#. As #a>0# the graph is a parabola that opens upward .

The requested points are connected by a smooth curve in the figure: the parabola that opens upward is given by the formula.

New example