Functies: Gebroken functies
 Asymptoten en hyperbolen
Asymptoten en hyperbolen
Bekijk de functie #f(x)=\tfrac{1}{x}#. In de grafiek zien we dat de functie uit twee takken bestaat. Dit komt doordat #0# niet in het domein van de functie ligt en #f(0)# dus niet bestaat. We noemen zo'n grafiek bestaande uit twee takken een #\blue{\textbf{hyperbool}}#.
We zien dat zowel als #x# heel klein wordt en zowel als #x# heel groot wordt de grafiek steeds dichter de #x#-as nadert. De functiewaarde wordt echter nooit gelijk aan #0#. We noemen de #x#-as, dat is de lijn #y=0#, de #\purple{\textbf{horizontale asymptoot}}# van de grafiek.
Ook zien we dat als de #x#-waarde vanaf de negatieve kant de #0# nadert dat de functiewaarde heel negatief wordt. Hoe dichter #x# bij #0# komt de liggen hoe negatiever de functiewaarde wordt. Als daarentegen de #x#-waarde vanaf de positieve kant steeds dichter #0# nadert, wordt #f(x)# steeds groter. We noemen de #y#-as, dat is de lijn #x=0#, de #\green{\textbf{verticale asymptoot}}# van de grafiek.
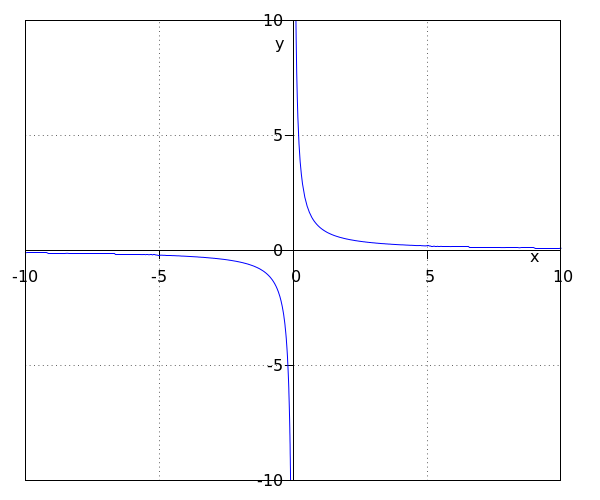
Asymptoot en hyperbool
Een asymptoot is een lijn die de grafiek van een functie steeds dichter nadert, maar waarmee de grafiek nooit samenvalt.
Een hyperbool is een functie waarbij de grafiek uit twee losse delen bestaat door een asymptoot. Deze twee losse delen noemen we de takken van de grafiek.
De horizontale asymptoot is: #y=0#
Immers, de verticale asymptoot vinden we door te kijken welke waarde voor #x# we niet mogen invullen. In een gebroken functie mag de noemer niet gelijk aan #0# zijn. Daarom is de verticale asymptoot gelijk aan #x=9#.
De horizontale asymptoot vinden we door heel grote waarden voor #x# in te vullen en te kijken wat er dan met de functie gebeurt. Als we voor #x# heel grote waarden invullen, dan wordt #x-9# heel groot. Vervolgens nadert #{{1}\over{x-9}}# steeds dichter de #0#, maar wordt dat nooit. Daarom is de horizontale asymptoot gelijk aan #y=0#.

omptest.org als je een OMPT examen moet maken.



