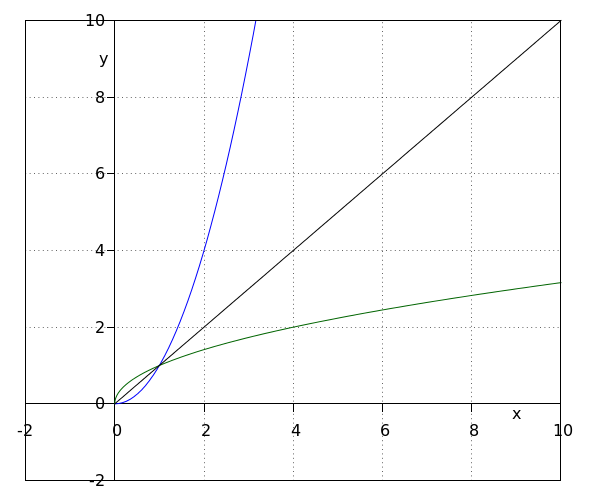
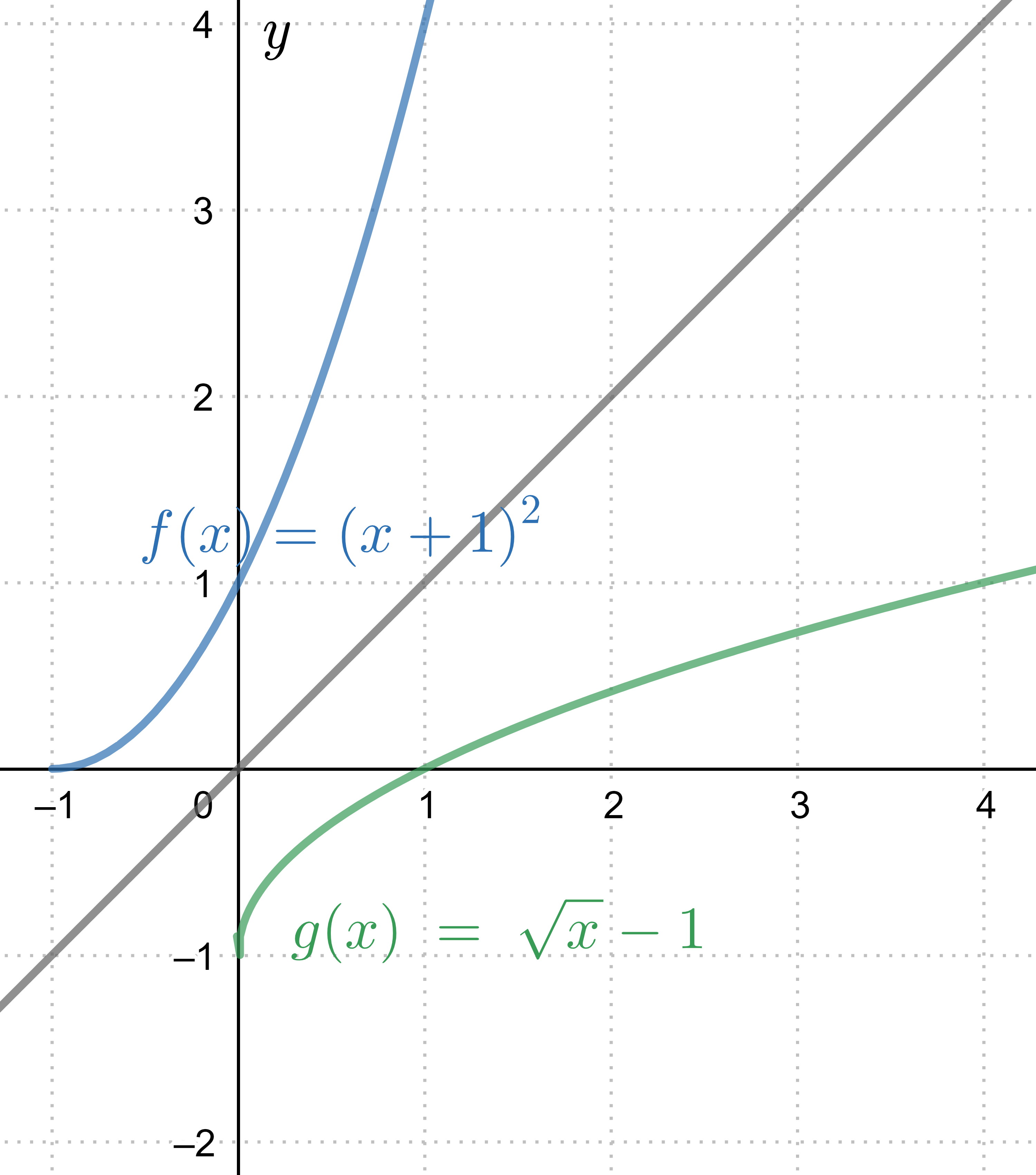We take a look at the functions #\blue{f(x)}=\blue{x^2}# (solid) and #\green{g(x)}=\green{\sqrt{x}}# (dashed) on the domain #\ivco{0}{\infty}#.
For these functions we have #\blue f(\green{g(x)})=\left(\green{\sqrt{x}}\right)^\blue2=x# for all #x# in #\ivco{0}{\infty}#.
Therefore #\green{g(x)}# is called the inverse of #\blue{f(x)}#.
We also have #\green g(\blue{f(x)})=\green{\sqrt{\blue{x^2}}}=x# for all #x# in #\ivco{0}{\infty}#.
Therefore #\blue{f(x)}# is called the inverse of #\green{g(x)}#.
The function #\blue{f(x)}# has inverse function #\green{g(x)}# if \[\blue f(\green{g(x)})=x\]
From a geometrical perspective, the graph of the inverse of #\green{g(x)}# is the reflection of #\blue{f(x)}# over the line #y=x#.
We can also notate the inverse of #f(x)# by #f^{-1}(x)#.
When determining the inverse of a function, the domain of that function is important. The domain of #\blue{f(x)}# is the range of #\green{g(x)}# and the domain of #\green{g(x)}# is the range of #\blue{f(x)}#. Hence, the inverse function #\green{g(x)}# is defined on the range of function #\blue{f(x)}#.
Example
In the graph #\blue{f(x)}=\blue{(x+1)^2}# on the domain #x \ge -1# and its inverse #\green{g(x)}=\green{\sqrt{x}-1}# on the domain #x \ge 0#
The domain of the function #\blue{f(x)}=\blue{(x+1)^2}# consists of all numbers and its range consists of all non-negative numbers. Its inverse function #\green{g(x)}=\green{\sqrt{x}-1}# has thus as domain only the non-negative numbers, where its range is also only the non-negative numbers. Hence, the function #\blue{f(x)}=\blue{(x+1)^2}# only has an inverse on the domain of all non-negative numbers.
The other way around we have that the function #\green{g(x)}=\green{\sqrt{x}-1}# has function #\blue{f(x)}=\blue{(x+1)^2}# as inverse, but only on the domain of all numbers greater than or equal to #-1#. Because, that is the range of #\green{g(x)}# and thus the domain of #\blue{f(x)}#.
We will usually not mention these limitations in the domain of the inverse function, but implicitly assume them.
| |
Procedure
We determine the inverse function #\green{f^{-1}(x)}# of the function #\blue{f(x)}#.
|
Example
#\blue{f(x)}=\left(x-4\right)^2#.
|
| Step 1 |
Write the function as a formula, hence in the form #y=\ldots#.
|
#y=\left(x-4\right)^2# |
| Step 2 |
Isolate the variable #x# in the formula #y=\ldots#. This means that the formula is written as #x=\ldots#.
|
#x=\sqrt{y}+4# |
| Step 3 |
In the formula, change the #y# into #x# and #x# into #y#.
|
#y=\sqrt{x}+4# |
| Step 4 |
Replace #y# by #\green{f^{-1}(x)}#.
|
#\green{f^{-1}(x)}=\sqrt{x}+4# |
We work out step 2 from the example. In there we want to isolate the variable #x# in the formula #y=\left(x-4\right)^2#. This is done by means of reduction.
\[\begin{array}{rcl}y&=&\left(x-4\right)^2 \\ &&\phantom{xxx}\blue{\text{original formula}} \\ \sqrt{y}&=&x-4 \\ &&\phantom{xxx}\blue{\text{both sides root extracted }} \\ \sqrt{y}+4&=&x \\ &&\phantom{xxx}\blue{\text{both sides plus }4}\end{array}\]
Therefore, #x=\sqrt{y}+4#.
Note that isolating a variable is actually the same as determining the inverse function.
In that case we don't have to go through step 3 and 4 anymore, and we are ready at step 2 of the procedure.
In step 2, we took the square root on both sides to be able to isolate #x# out of the square. We take the positive root. As we saw in the introduction of the root function the root of a non-negative number is a non-negative number.
If a certain domain is specified for finding the inverse, it could be necessary to take the negative root. In the example, #\blue{f(x)}# has a domain of all real numbers and a range of all non-nagative numbers. The inverse function #\green{f^{-1}(x)}# has as domain all non-negative numebrs and as range all number greater than or equal to #4#. Thus, only on the domain #x \ge 4# does #\blue{f(x)} = \blue{(x-4)^2}# have the inverse #\green{f^{-1}(x)} = \green{\sqrt{x}+4}#.
If we were asked to calculate the inverse of #\blue{f(x)}# on the domain #x\le 4# then we should have taken the negative root in step 2. The inverse of #\blue{f(x)} =\blue{ (x-4)^2}# on the domain #x \le 4# is #\green{f^{-1}(x) }= \green{-\sqrt{x}+4}#. this function has as domain all non-negative numbers and as range all number less than or equal to #4#, which is exactly the given domain.
Isolate #x# in
\[y=\sqrt{1-2\cdot x}\]
Give your answer in the form #x = ...#
#x={{1-y^2}\over{2}}#
#\begin{array}{rcl}
y&=&\sqrt{1-2\cdot x} \\ &&\phantom{xxx}\blue{\text{original function}}\\
y^2&=& 1-2\cdot x \\ &&\phantom{xxx}\blue{\text{both sides squared}}\\
y^2-1&=&-2\cdot x \\ &&\phantom{xxx}\blue{\text{both sides minus }1}\\
{{1-y^2}\over{2}} &=&x \\ &&\phantom{xxx}\blue{\text{both divided by }-2}\\
x&=&{{1-y^2}\over{2}} \\ &&\phantom{xxx}\blue{\text{left and right swapped }}\\
\end{array}#
Inverse functions
