Functions: Fractional functions
 Power functions with negative exponents
Power functions with negative exponents
Power function with negative exponent
A power function with a negative integer exponent has the form \[f(x)=\blue{a}x^{-\orange{n}}\]
in which #\orange{n}# is a postive integer.
We can also write this function as \[f(x)=\frac{\blue{a}}{x^{\orange{n}}}\]
The graph of a power function with a negative integer exponent moves through the point #\rv{1,\blue{a}}#, has a vertical asymptote at #x=0# and a horizontal asymptote in the line #y=0#.
If #\orange{n}# is even, the function is symmetrical across the #y#-axis. If #\orange{n}# is odd, the function has the point #\rv{0,0}# as the point of symmetry.
GeoGebra Negative powerfunction
Take a look at the graph of a power function with a negative exponent, which is a function of the form #f(x)=\frac{a}{x^n}#.
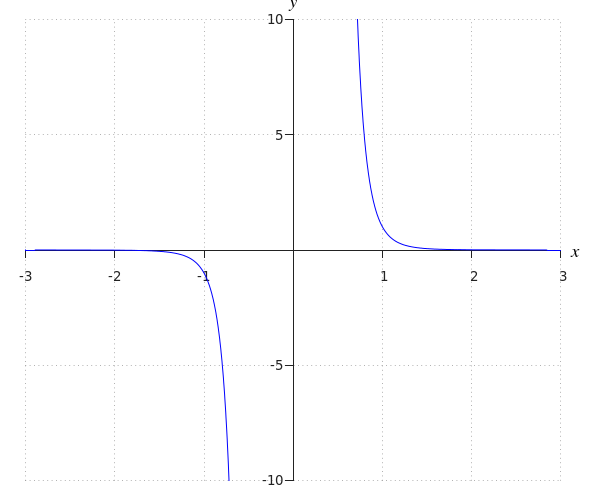
What do we know about the values of #n# and #a#?

What do we know about the values of #n# and #a#?
The value of #n# is: odd
The value of #a# is: positive
The graph is symmetrical across the point #\rv{0,0}#, hence, the value of #n# is odd.
The #y#-value is positive if the value of #x# is positive, hence the value of #a# is positive.
The value of #a# is: positive
The graph is symmetrical across the point #\rv{0,0}#, hence, the value of #n# is odd.
The #y#-value is positive if the value of #x# is positive, hence the value of #a# is positive.
Unlock full access


Teacher access
Request a demo account. We will help you get started with our digital learning environment.
Student access
Is your university not a partner?
Get access to our courses via Pass Your Math independent of your university. See pricing and more.
Or visit omptest.org if jou are taking an OMPT exam.
Or visit omptest.org if jou are taking an OMPT exam.



