Trigonometric functions

Trigonometry: Trigonometric functions

Trigonometric functions

The sine, cosine and tangent are not only used at angles, but can also be used as a function.

Sine function

The sine function #f(x)=\sin(x)# is the function that adds the sine of #x# to each number #x#.

As we have seen in the unit circle, the function repeats every #2 \pi#. We therefore call the sine function a periodic function with #\blue{\text{period}}# #2 \pi#.

The function also has an #\green{\text{equilibrium}}#. This is the middle of the function, or the #y#-value that lies exactly between the highest and the lowest point. For the sine function, this is #0#.

Finally, the #\purple{\text{amplitude}}# of the function is equal to #1#. This means that the value between the equilibrium and the highest point (or the lowest point) equals #1#.

In words At Angles in radians we saw that the sine of an angle #\alpha# is defined as the #y#-coordinate of the point on the unit circle corresponding with the angle #\alpha#.

We now interpret the sine as a function. To a value #x# it assigns the value of the sine of the angle of #x# radians. This means we get a periodic function, with the angle on the #x#-axis.

Summarized: the sine function has the angle in radians on the #x# axis, and the #y#-coordinate of the corresponding point on the unit circle on the #y#-axis.

Cosine function

The cosine function #f(x)=\cos(x)# is the function that adds the cosine of #x# radians to each number #x#.

Like the sine function, the cosine function is a periodic function. This too has #\blue{\text{period}}# #2\pi#.

The #\green{\text{equilibrium}}# is equal to #0#.

Additionally, the #\purple{\text{amplitude}}# of the function is equal to #1#.

When we compare the cosine function with the sine function, we see that the graphs are very similar. When we move the cosine function to the right by #\frac{\pi}{2}#, we have the sine function.

In words At Angles in radians we saw that the cosine of an angle #\alpha# is defined as the #x#-coordinate of the point on the unit circle corresponding with the angle #\alpha#.

We now interpret the cosine as a function. To a value #x# it assigns the value of the cosine of the angle of #x# radians. This means we get a periodic function, with the angle on the #x#-axis.

Summarized: the cosine function has the angle in radians on the #x# axis, and the #x#-coordinate of the corresponding point on the unit circle on the #y#-axis.

Tangent function

The tangent function #f(x)=\tan(x)# is the function that adds the tangent of #x# radians to each number #x#.

Like the sine and cosine functions, the tangent function is a periodic function. The #\blue{\text{period}}# is equal to #\pi#.

The vertical asymptotes of the tangent function are #x=\frac{\pi}{2}+k \cdot \pi#, in which #k# is an integer, as for the #x#-values #\frac{\pi}{2}#, #\frac{3 \pi}{2}# and #\frac{5 \pi}{2}#, but also for #\frac{-3 \pi}{2}#.

Consider the graph below.

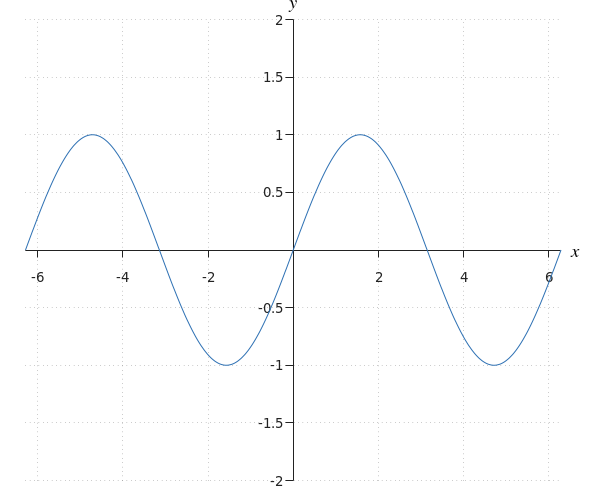
To which function does this graph belong?

#f(x)=\sin \left(x\right)#

We see a function with its equilibrium equal to #0#, period #2 \pi# and amplitude #1#. Furthermore, the function passes through the point #\rv{0,0}#. This means the function is equal to #f(x)=\sin \left(x\right)#.

New example