Area

Integration: The definite integral

Area

The area of the surface #\orange S# above the #x#-axis and bound by the graph of #\blue{f}#, the lines #x=a# and #x=b# is equal to

\[\int_a^b \blue f(x) \; \dd x\]

Plaatje hoofdblok

We will name the area of a fixed starting point till #x# below #\blue f# and above the #x#-axis #\orange A(x)# (see the figure on the right).

We will first prove that #\orange A(x)# is a primitive of #\blue f#. To prove that we show that #A'(x)=\blue{f}(x)#.

From the derivative definition:

\[A'(x)=\frac{\orange A(x+h)-\orange A(x)}{h} \text{ with } h \to 0\]

Plaatje 1

The area of #\orange A(x+h)-\orange A(x)# can be seen in the figure on the right hand side. For small values of #h# the purple part can be approximated with a rectangle with sides #h# and #\blue f(x)#. This means

\[\orange A(x+h)-\orange A(x) \approx \blue f(x) \cdot h\]

By dividing both sides by #h#, we find

\[\blue f(x) \approx \frac{\orange A(x+h)-\orange A(x)}{h}\]

When we let #h \to 0#, we indeed see that \[\blue f(x)=A'(x)\]

With this we have proven that #\orange A(x)# is a primitive of #\blue f#.

image 2

Finally, we see in the figure on the right hand side the situation in which we want to know the area of #a# to #b# below #\blue f#. We can see this area is equal to #\orange A(b)-\orange A(a)#.

Since #\orange A(x)# is a primitive of #\blue f(x)#, using the definition of the definite integral, the area of #a# to #b# under #f# is equal to: \[\orange A(b)-\orange A(a)=\int_a^b \blue f(x) \; \dd x\]

image 3

Application in physics

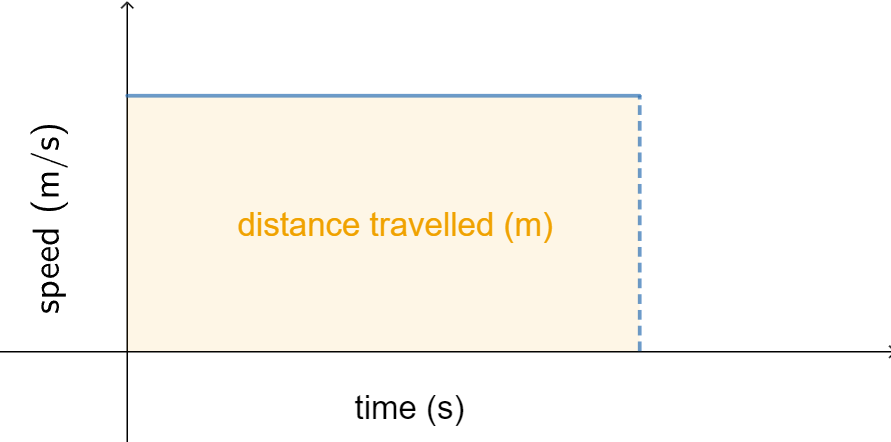
In Physics, we can use integration to calculate the distance travelled. Speed is measured as the distance travelled per unit of time, hence, given a constant speed and time period, the distance travelled in that time can be found by multiplying the speed and the period.

In the image, the constant speed function is graphed with time along the #x#-axis. The area between this speed function above the horizontal #t#-axis, and between the lines #t=#start time and #t=#end time is a rectangle, which has an area of length (time) times height (speed).

In other words, the distance travelled is the same as the area of the surface under the graph of the speed function in that period. This also applies to the case of non-constant speed.

Example
Assume a plane lifts off and for the first #20# seconds it has a speed of #v(t)=\frac{1}{2}t^2#, then the area of the surface enclosed by #v(t)# and the lines #t=0# and #t=20# is equal to the distance travelled in those first #20# seconds.

\[\int_{0}^{20}v(t)\, \dd t=\int_{0}^{20}\frac{1}{2}t^2\, \dd t =\left[\frac{1}{6}t^3\right]_{0}^{20}=\frac{4000}{3}\]

Hence, the plane travelled approximately #1330# meters in the first #20# seconds.

Application in economics

Integration is often used in economics to find the sum total of a function within a given period. For example, consider a company that brings a new game console to the market. The daily sales of this console are described by the function

\[Q(t) = 5500 \cdot 0.98^t \]

where #Q(t)# is the quantity of game consoles sold on day #t#.

Suppose we want to find the total number of game consoles sold in the first #30# days. We can calculate the sum total of #Q(t)# within the given period using the integral:

\[\int_{0} ^{30} Q(t) \, \dd t =\int_{0} ^{30} 5500 \cdot 0.98^t \, \dd t = \left[ \dfrac{5500}{\ln (0.98)} {0.98}^t \right]_{0}^{30} \approx 123738 \]

which we notice is equal to the area of the surface enclosed by the graph of #Q#, the horizontal #t#-axis and the lines #t=0# and #t=30#.
Therefore, the total number of game consoles sold in the first #30# days is #123738#.

Approximation

The area under the graph can be approximated by a rectangle, whose area is calculated as width #\times# height.

We can improve the approximation if we split the area and use more rectangles, the sum of the areas of the rectangles approaches the total area. The more rectangles we use, and thus the smaller they are, the better the approximation.

Using so many rectangles that their width approaches zero will make the approximation approach the total area. Move the slider in the image to visualise this.

GeoGebra

As a formula, let #x_i = x_s + i \cdot \Delta x#, and #x_s = x_0# and #x_e = x_s + n \cdot \Delta x#, then, when #\Delta x \rightarrow 0#,
\[ \green{A} = \blue f(x_1) \cdot \Delta x + \blue f(x_2) \cdot \Delta x + \ldots + \blue f(x_{n-1}) \cdot \Delta x + \blue f(x_e) \cdot \Delta x \approx \int_{x_s}^{x_e} \blue f(x) \, \dd x = \orange S\]

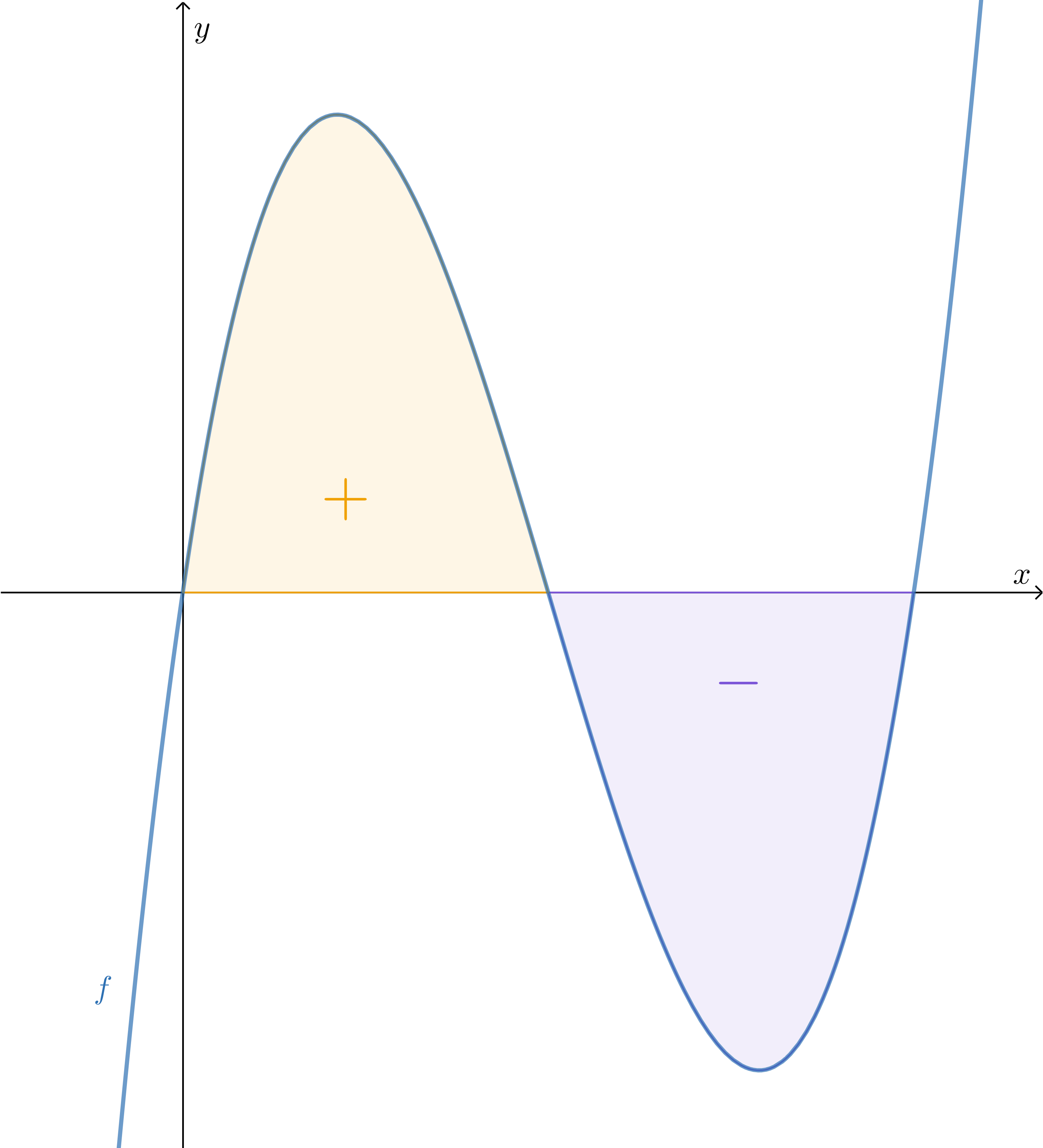
We have now seen how to calculate the area of a surface above the #x#-axis, but in the same manner, we can calculate a surface below the #x#-axis.

The area of the surface #\orange S# that lies below the #x#-axis and is enclosed by the graph of #\blue{f}#, the lines #x=a# and #x=b# is equal to:

\[-\int_a^b \blue f(x) \; \dd x\]

main image 2

In the same manner, as we have shown for a surface above the #x#-axis, we can show that #\int_a^b \blue f(x) \; \dd x# is equal to #-(\text{area})#.

Signed area

In this course, we consider an area always non-negative. The area between a graph below the #x#-axis and the #x#-axis is determined by taking the absolute value of the definite integral.

We can say that the definite integral indicates the position or direction of the area. If we calculate the area between a graph and the #x#-axis, between two consecutive intersection points with the #x#-axis, as the definite integral and the outcome is negative, it means the area is below the #x#-axis.

We call the definite integral the signed area.

Finally, we will present a procedure for how to calculate the area enclosed by the graph of #\blue f#, the #x#-axis and the lines #x=a# and #x=b#. Here, the area can be partly above and partly below the graph.

	Procedure	Example
	Determine the area of a surface enclosed by the graph #\blue f#, the #x#-axis and the lines #x=a# and #x=b#.	The area enclosed by #\blue f(x)=-(x-3)^2+4#, the #x#-axis and #x=0# and #x=6#
Step 1	Determine the zeros of the graph of #\blue f# between #x=a# and #x=b#. We will name these zeros #x_1#, #x_2#, #\ldots#, #x_n# if there are #n# zeros.	#x_1=1#, #x_2=5#
Step 2	For every interval #\ivco{a}{x_1}#, #\ivoo{x_1}{x_2}#, #\ldots#, #\ivoc{x_n}{ b}# determine if the #y#-values of #f# are positive or negative.	\[f(x)\begin{cases}\lt0&\text{als } x \text{ in } \ivco{0}{1}\\ \gt0&\text{if } x \text{ in } \ivoo{1}{5} \\ \lt 0 &\text{if } x \text{ in } \ivoc{5}{6}\end{cases} \]
Step 3	The area of the surface is equal to: \[\pm \int_a^{x_1} \blue f (x)\; \dd x \pm \int_{x_1}^{x_2} \blue f (x)\; \dd x \pm \ldots \pm \int_{x_n}^{b} \blue f(x) \; \dd x \] Here, we have a plus sign in front of the integral if #f# is positive for that domain and a minus sign if #f# is negative.	\[\begin{array}{c}-\int_{0}^{1} (x-3)^2+4 \; \dd x \\ + \int_{1}^{5} (x-3)^2+4 \; \dd x \\ - \int_{5}^6 (x-3)^2+4 \; \dd x\end{array}\]
Step 4	Calculate the definite integrals and determine the area.	#\frac{46}{3}#

Graphical

In the figure below, the area of the orange colored part is what we calculated in the example.

Plaatje stappenplan

The figure below shows the graph of the function #f(x)=x^2+3\cdot x-4# drawn for #x\in\ivcc{-4}{6}#. The region enclosed by the function #f# and the #x#-axis is colored gray.

Calculate the area of the enclosed domain.
Give your answer as simplified fraction.

#125#

Step 1	The only zero of #f(x)=x^2+3\cdot x-4# between #x=-4# and #x=6# is #x_1=1#. The other zero of the polynomial is #x=-4#, but this does not matter for the calculation.
Step 2	For #[-4,1)#, #f(x)# is negative, for #[1,6)# #f(x)# is positive.
Step 3	The area of the surface is equal to \[-\int_{-4}^{1} f(x) \, \dd x+ \int_{1}^{6}f(x) \, \dd x\]
Step 4	We calculate the definite integrals. \[\begin{array}{rcl}\displaystyle \int_{-4}^{1} x^2+3\cdot x-4 \, \dd x &=&\displaystyle\left[{{x^3}\over{3}}+{{3\cdot x^2}\over{2}}-4\cdot x\right]_{-4}^{1}\\ &&\phantom{xxx}\blue{\text{definition definite integral}}\\ &=&\displaystyle -{{13}\over{6}} - {{56}\over{3}}\\ &&\phantom{xxx}\blue{\text{entering of boundaries and simplification}}\\ &=&\displaystyle -{{125}\over{6}}\\ &&\phantom{xxx}\blue{\text{simplified}} \end{array}\] \[\begin{array}{rcl}\displaystyle \int_{1}^{6} x^2+3\cdot x-4 \, \dd x &=&\displaystyle\left[{{x^3}\over{3}}+{{3\cdot x^2}\over{2}}-4\cdot x\right]_{1}^{6}\\ &&\phantom{xxx}\blue{\text{definition definite integral}}\\ &=&\displaystyle 102 +{{13}\over{6}}\\ &&\phantom{xxx}\blue{\text{entering of boundaries and simplification}}\\ &=&\displaystyle {{625}\over{6}}\\ &&\phantom{xxx}\blue{\text{simplified}} \end{array}\] We enter this and hence we find the area we are looking for \[\begin{array}{rcl}\displaystyle -\int_{-4}^{1} f(x) \, \dd x+ \int_{1}^{6}f(x) \, \dd x&=&\displaystyle -(-{{125}\over{6}})+{{625}\over{6}}\\&=&\displaystyle 125 \end{array}\]

New example