De oppervlakte van het vlakdeel #\orange S# (we gebruiken #\orange S# wegens het Engelse woord "surface") dat boven de #x#-as ligt en wordt ingesloten door de grafiek van #\blue{f}#, de lijnen #x=a# en #x=b# is gelijk aan
\[\int_a^b \blue f(x) \; \dd x\]
|
We noemen de oppervlakte van een vast startpunt tot #x# onder #\blue f# en boven de #x#-as #\orange A(x)# (#\orange A#, wegens het Engelse woord voor oppervlakte "area", zie figuur rechts).
We gaan eerst bewijzen dat #\orange A(x)# een primitieve is van #\blue f#. Om dat de te bewijzen tonen we aan dat #A'(x)=\blue{f}(x)#.
Wegens de definitie van de afgeleide geldt:
\[A'(x)=\frac{\orange A(x+h)-\orange A(x)}{h} \text{ met } h \to 0\]
|
Plaatje 1
|
|
De oppervlakte van #\orange A(x+h)-\orange A(x)# is te zien in de figuur rechts. Voor kleine waarden van #h# is het paarse deel te benaderen met een rechthoek met zijden #h# en #\blue f(x)#. Dit betekent
\[\orange A(x+h)-\orange A(x) \approx \blue f(x) \cdot h\]
Door beide kanten te delen door #h#, vinden we
\[\blue f(x) \approx \frac{\orange A(x+h)-\orange A(x)}{h}\]
Wanneer we #h \to 0# laten gaan, zien we dus inderdaad dat \[\blue f(x)=A'(x)\]
Hiermee is bewezen dat #\orange A(x)# een primitieve van #\blue f# is.
|
Plaatje 2
|
|
Tot slot zien we in de figuur rechts de situatie dat we de oppervlakte van #a# naar #b# onder #\blue f# willen weten. We zien dat deze oppervlakte gelijk is aan #\orange A(b)-\orange A(a)#.
Omdat #\orange A(x)# een primitieve is van #\blue f(x)#, is, volgens de definitie van de bepaalde integraal, de oppervlakte van #a# naar #b# onder #f# gelijk aan: \[\orange A(b)-\orange A(a)=\int_a^b \blue f(x) \; \dd x\]
|
Plaatje 3
|
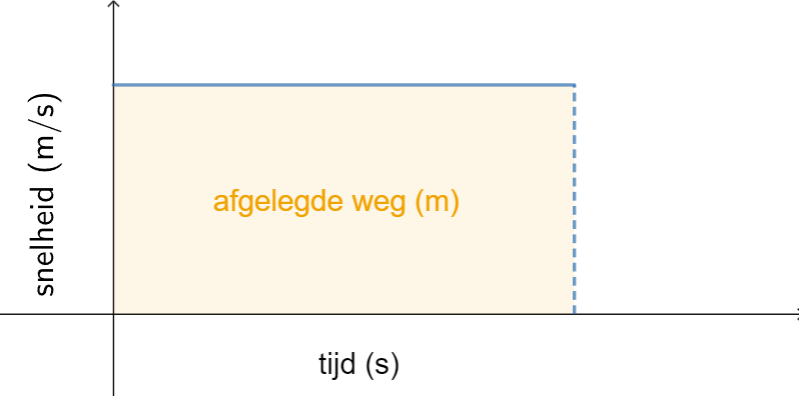
We kunnen integratie gebruiken om de afgelegde afstand te berekenen. Snelheid wordt gemeten als de afgelegde weg per tijdseenheid. Gegeven een constante snelheid en een tijdsperiode, wordt de afgelgde weg berekend door de snelheid te vermenigvuldigen met de verstreken tijd.
In de afbeelding is de snelheidsfuntie getekend met de tijd op de #x#-as. De oppervlakte tussen deze snelhiedsgrafiek, de horizontale tijdsas en de lijnen #t=#start tijd en #t=#eind tijd is een rechthoed, die een oppervlakte heeft van lengte (tijd) keer hoogte (snelheid).
Met andere woorden, de in een bepaalde tijd afgelgde afstand is hetzelfde als de oppervlakte van het vlakdeel ingesloten door de snelheidsgrafiek en die tijdsperiode. Dit gaat ook op in het geval de snelheid niet constant is.
Voorbeeld
Stel een vliegtuig stijgt op en heeft in de eerste #20# seconden een snelheid van #v(t)=\frac{1}{2}t^2#, dan komt de oppervlakte van het vlak dat wordt ingesloten door #v(t)# en de lijnen #t=0# en #t=20# overeen met de afgelegde afstand in die eerste #20# seconden.
\[\int_{0}^{20}v(t)\, \dd t=\int_{0}^{20}\frac{1}{2}t^2\, \dd t =\left[\frac{1}{6}t^3\right]_{0}^{20}=\frac{4000}{3}\]
Het vliegtuig heeft dus een afstand van ongeveer #1330# meter afgelegd in de eerste #20# seconden.
Integratie wordt vaak in de economie gebruikt om het totaal van een functie in een bepaalde periode te berekenen. Bijvoorbeeld, neem een bedrijf dat een nieuwe spelcomputer op de markt brengt. De dagelijkse verkoop van deze spelcomputer wordt beschreven door de functie
\[Q(t) = 5500 \cdot 0.98^t \]
waar #Q(t)# de hoeveelheid verkochte spelcomputers op dag #t# is.
Stel dat we willen weten hoeveel spelcomputers in totaal verkocht zijn in de eerste #30# dagen, dan kunnen we de totale som van #Q(t)# in deze periode berekenen met de integraal
\[\int_{0} ^{30} Q(t) \, \dd t =\int_{0} ^{30} 5500 \cdot 0.98^t \, \dd t = \left[ \dfrac{5500}{\ln (0.98)} {0.98}^t \right]_{0}^{30} \approx 123738 \]
Merk op dat dit gelijk is aan de oppervlakte van het vlakdeel ingesloten door de grafiek van #Q#, de horizontale #t#-as en de lijnen #t=0# en #t=30#.
Het totaal aantal verkochte spelcomputers in de eerste #30# dagen is dus #123738#.
De oppervlakte onder een grafiek kan worden benaderd door een rechthoek, waarvan de oppervlakte breedte #\times# hoogte is.
We kunnen de benadering verbeteren door meer rechthoeken te gebruiken, de som van de oppervlakten van de rechthoeken benaderen de totale oppervlakte onder de grafiek. Hoe meer rechthoeken we gebruiken, en dus hoe smaller deze zijn, des te beter wordt de benadering.
Als we zoveel rechthoeken gebruiken dat hun breedte naar nul nadert, zal de som van hun oppervlakten naar de werkelijke oppervlakte onder de grafiek naderen. Beweeg de schuif in de afbeelding om dit te zien.
In formulevorm, laat #x_i = x_s + i \cdot \Delta x#, en #x_s = x_0# en #x_e = x_s + n \cdot \Delta x#, dan, als #\Delta x \rightarrow 0#,
\[ \green{A} = \blue f(x_1) \cdot \Delta x + \blue f(x_2) \cdot \Delta x + \ldots + \blue f(x_{n-1}) \cdot \Delta x + \blue f(x_e) \cdot \Delta x \approx \int_{x_s}^{x_e} \blue f(x) \, \dd x = \orange S\]
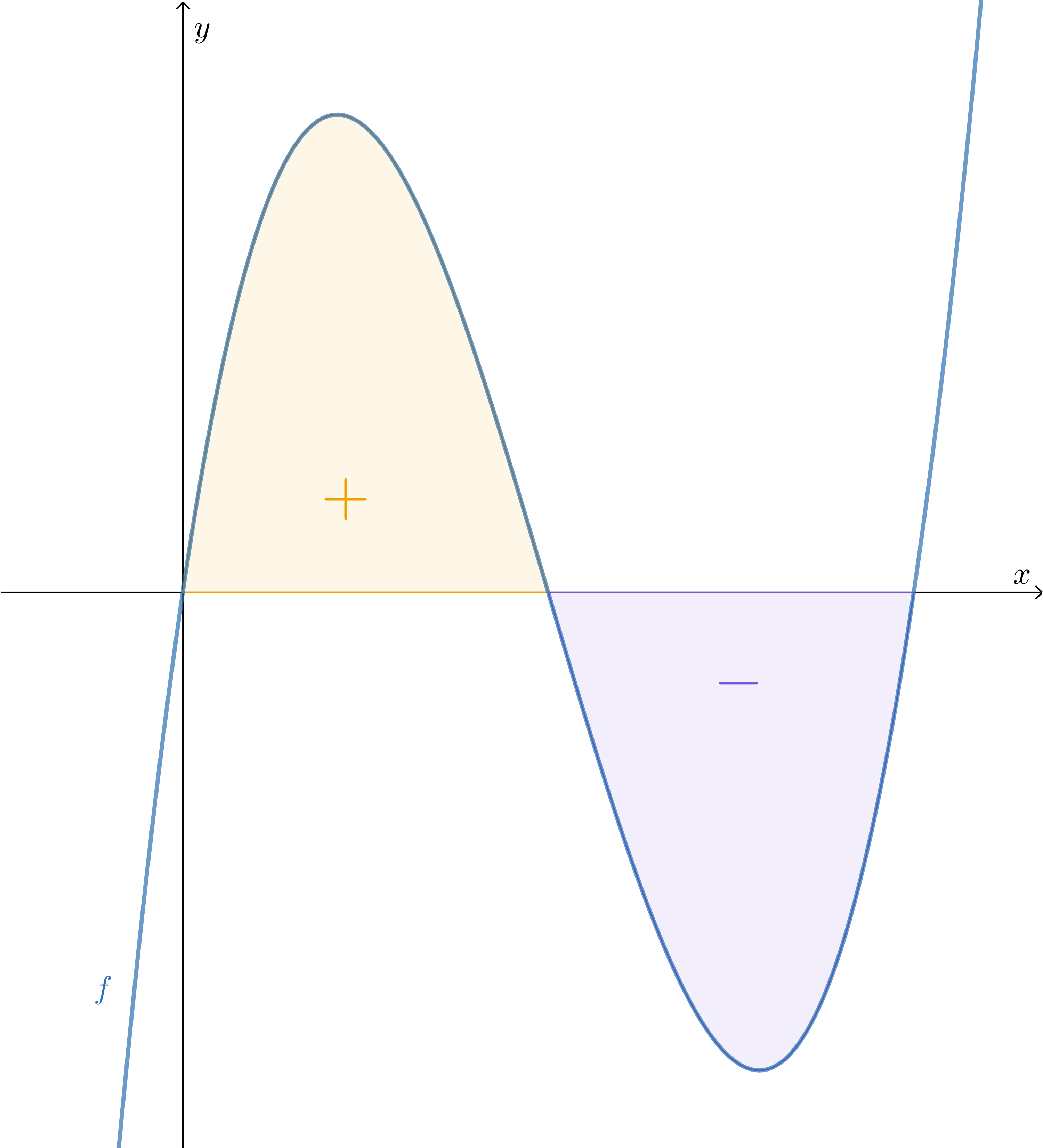
We hebben nu gezien hoe we de oppervlakte van een vlakdeel boven de #x#-as berekenen, maar we kunnen op soortgelijke wijze ook een vlakdeel onder de #x#-as berekenen.
De oppervlakte van het vlakdeel #\orange S# dat onder de #x#-as ligt en wordt ingesloten door de grafiek van #\blue{f}#, de lijnen #x=a# en #x=b# is gelijk aan:
\[-\int_a^b \blue f(x) \; \dd x\]
Op soortgelijke wijze als bij een vlakdeel boven de #x#-as kunnen we laten zien dat #\int_a^b \blue f(x) \; \dd x# gelijk is aan #-(\text{oppervlakte})#.
In deze cursus beschouwen we de oppervlakte altijd als niet-negatief. De oppervlakte van het vlakdeel ingesloten door een grafiek onder de #x#-as en de #x#-as wordt berekend door de absolute waarde te nemen van de bepaalde integraal.
We kunnen stellen dat de bepaalde integraal de positie of de richting van de oppervlakte weergeeft. Als we de oppervlakte tussen een grafiek en de #x#-as, tussen twee opvolgende snijpunten met de #x#-as, met behulp van de bepaalde integraal berekenen en de uitkomst is negatief, dan betekent dat dat de oppervlakte onder de #x#-as ligt.
We noemen de bepaalde integraal de georiënteerde oppervlakte.
Tot slot zullen we een stappenplan geven hoe we van een grafiek de oppervlakte kunnen geven die ingesloten wordt door de grafiek van #\blue f#, de #x#-as en door de lijnen #x=a# en #x=b#. Hierbij kan de oppervlakte gedeeltelijk boven de grafiek en gedeeltelijk onder de grafiek liggen.
| |
Stappenplan |
Voorbeeld
|
| |
Bepaal de oppervlakte van een gebied ingesloten door de grafiek #\blue f#, de #x#-as en de lijnen #x=a# en #x=b#.
|
Het gebied ingesloten door #\blue f(x)=-(x-3)^2+4#, de #x#-as en #x=0# en #x=6#
|
| Stap 1 |
Bepaal de nulpunten van de grafiek van #\blue f# tussen #x=a# en #x=b#. We noemen de nulpunten #x_1#, #x_2#, #\ldots#, #x_n# als er #n# nulpunten zijn.
|
#x_1=1#, #x_2=5# |
| Stap 2 |
Bepaal voor elk interval #\ivco{a}{x_1}#, #\ivoo{x_1}{x_2}#, #\ldots#, #\ivoc{x_n}{ b}# of de #y#-waarden van #f# positief of negatief zijn. |
\[f(x)\begin{cases}\lt0&\text{als } x \text{ in } \ivco{0}{1}\\
\gt0&\text{als } x \text{ in } \ivoo{1}{5}
\\ \lt 0 &\text{als } x \text{ in } \ivoc{5}{6}\end{cases}
\]
|
| Stap 3 |
De oppervlakte van het gebied is gelijk aan:
\[\pm \int_a^{x_1} \blue f(x) \; \dd x \pm \int_{x_1}^{x_2} \blue f (x)\; \dd x \pm \ldots \pm \int_{x_n}^{b} \blue f (x)\; \dd x \]
Hierbij staat er een plusteken voor de integraal als #f# positief is op dat gebied en een minteken als #f# negatief is.
|
\[\begin{array}{c}-\int_{0}^{1} \left(-(x-3)^2+4 \right) \dd x \\ + \int_{1}^{5} \left(-(x-3)^2+4 \right) \dd x \\ - \int_{5}^6 \left(-(x-3)^2+4 \right) \dd x\end{array}\] |
| Stap 4 |
Bereken de bepaalde integralen en bepaal zo de oppervlakte.
|
#\frac{46}{3}# |
De oppervlakte van het oranje gekleurde gedeelte in de figuur hieronder is wat we in het voorbeeld berekend hebben.
Plaatje stappenplan
In de figuur hieronder is de grafiek van de functie #f(x)=x^2-8\cdot x+12# getekend voor #x\in\ivcc{2}{9}#. Het gebied ingesloten door de functie #f# en de #x#-as is grijs gekleurd.
Bereken de oppervlakte van het ingesloten gebied.
Geef je antwoord als onvereenvoudigbare breuk.
#\frac{113}{3}#
| Stap 1 |
Het enige nulpunt van #f(x)=x^2-8\cdot x+12# tussen #x=2# en #x=9# is #x_1=6#. Het andere nulpunt van het polynoom is #x=2#, maar dit maakt niet uit voor de berekening. |
| Stap 2 |
Voor #[2,6)# is #f(x)# negatief, voor #[6,9)# is #f(x)# positief. |
| Stap 3 |
De oppervlakte van het gebied is gelijk aan
\[-\int_{2}^{6} f(x) \, \dd x+ \int_{6}^{9}f(x) \, \dd x\] |
| Stap 4 |
We berekenen de bepaalde integralen.
\[\begin{array}{rcl}\displaystyle
\int_{2}^{6} x^2-8\cdot x+12 \, \dd x &=&\displaystyle\left[{{x^3}\over{3}}-4\cdot x^2+12\cdot x\right]_{2}^{6}\\
&&\phantom{xxx}\blue{\text{definitie bepaalde integraal}}\\
&=&\displaystyle 0 - {{32}\over{3}}\\
&&\phantom{xxx}\blue{\text{grenzen ingevuld en vereenvoudigd}}\\
&=&\displaystyle -{{32}\over{3}}\\
&&\phantom{xxx}\blue{\text{vereenvoudigd}}
\end{array}\]
\[\begin{array}{rcl}\displaystyle
\int_{6}^{9} x^2-8\cdot x+12 \, \dd x &=&\displaystyle\left[{{x^3}\over{3}}-4\cdot x^2+12\cdot x\right]_{6}^{9}\\
&&\phantom{xxx}\blue{\text{definitie bepaalde integraal}}\\
&=&\displaystyle 27 - 0\\
&&\phantom{xxx}\blue{\text{grenzen ingevuld en vereenvoudigd}}\\
&=&\displaystyle 27\\
&&\phantom{xxx}\blue{\text{vereenvoudigd}}
\end{array}\]
We vullen dit in en vinden de gezochte oppervlakte
\[\begin{array}{rcl}\displaystyle -\int_{2}^{6} f(x) \, \dd x+ \int_{6}^{9}f(x) \, \dd x&=&\displaystyle -(-{{32}\over{3}})+27\\&=&\displaystyle \frac{113}{3} \end{array}\] |
 Oppervlakte
Oppervlakte