Quadratic equations: Parabola
Parabola
Graph
The graph of a quadratic \[y=\blue ax^2+\green bx+\purple c\] is called a parabola.
If #\blue a \gt 0# the graph is an upward opening parabola.
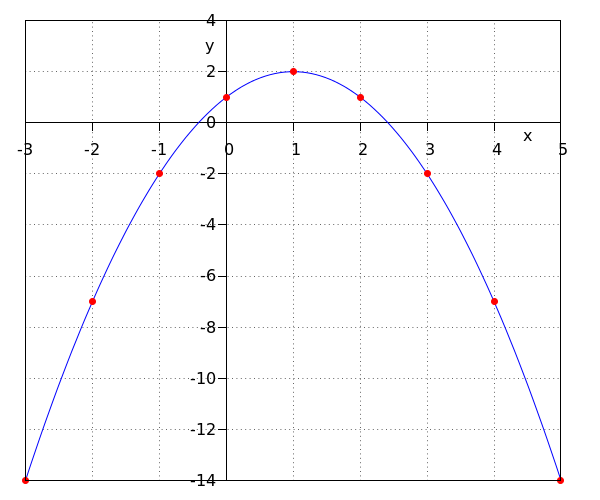
If #\blue a \lt 0# the graph is a downward opening parabola.
An upward opening parabola has a minimum and downward opening parabola has a maximum. In both cases, this point is referred to as the vertex of the graph.
The parabola is symmetrical about the vertical line through the top of the graph. Such a line is also called a #\orange{\textbf{line of symmetry}}#.
To plot the graph of the quadratic #y=-x^2+2x+1#, start by constructing a table. Next, draw the points in a coordinate system and connect the dots with a smooth curve.
Table
#\begin{array}{l|c|c|c|c|c|c|c|c|c} x & -3 & -2 & -1 & 0 & 1 & 2 & 3&4&5\\ \hline y & -14 & -7 & -2 & 1 & 2 & 1 & -2 &-7 & -14 \end {array}#
We find the values of #y# by plugging the values of #x# into the formula.
Chart
Draw the points in the coordinate system and connect them with a smooth curve.
We substitute #x=-10# in the formula. This is done in the following way:
\[y=-8\cdot (-10)^2+56\cdot (-10)-80=-1440\]
Hence #\rv{-10, -1431}# does not lie on the graph.
Or visit omptest.org if jou are taking an OMPT exam.
