Equations with power functions

Functions: Power functions

Equations with power functions

In quadratic equations, we have seen how to solve an equation #x^2=c#. With the same procedure, we will use higher degree roots to solve an equation #x^n=c#.

The solutions to the equation #x^\orange{n}=\blue{c}# are dependent on the values of #\orange n# and #\blue c#.

#\blue{c} \gt 0#

#\blue{c}=0#

#\blue{c} \lt 0#

#\orange{n}# is even

Two solutions:

#x=-\sqrt[\orange{n}]{\blue{c}} \lor x=\sqrt[\orange{n}]{\blue{c}}#

One solution:

#x=0#

No solutions

#\orange{n}# is odd

One solution:

#x=\sqrt[\orange{n}]{\blue{c}}#

One solution:

#x=0#

One solution:

#x=\sqrt[\orange{n}]{\blue{c}}#

Fractional powersPlease remember that we have seen the following rule with Fractional powers:

\[\sqrt[\orange{n}]{x}=x^{\frac{1}{\orange{n}}}\]

Therefore, we can also write the solutions with a fractional power. The solutions then look like this:

#\blue{c} \gt 0#

#\blue{c}=0#

#\blue{c} \lt 0#

#\orange{n}# is even

Two solutions:

#x=-\blue{c}^{\frac{1}{\orange{n}}} \lor x=\blue{c}^{\frac{1}{\orange{n}}}#

One solution:

#x=0#

No solutions

#\orange{n}# is odd

One solution:

#x=\blue{c}^{\frac{1}{\orange{n}}}#

One solution:

#x=0#

One solution:

#x=\blue{c}^{\frac{1}{\orange{n}}}#

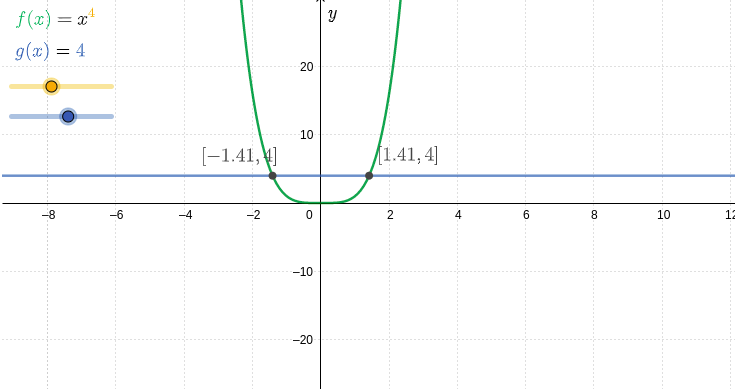
In the examples, we see that you can reduce many equations to the form #x^\orange{n}=\blue{c}# and then solve them.

Solve #5\, x^{2}+5=8# for #x#.

Give your answer in the form #x=x_1# or #x=x_1 \lor x=x_2# for suitable numbers #x_1# and #x_2#.

#x=\frac{1}{5}\sqrt{15} \lor x=-\frac{1}{5}\sqrt{15}#

#\begin{array}{rcl}5\, x^{2}+5&=& 8 \\
&&\phantom{xxx}\blue{\text{the equation we need to solve}} \\
5\, x^{2}&=&3 \\
&&\phantom{xxx}\blue{\text{both sides minus }5} \\
x^{2} &=& {{3}\over{5}} \\
&&\phantom{xxx}\blue{\text{both sides divided by }5} \\
x=\sqrt[2]{{{3}\over{5}}} &\lor& x=-\sqrt[2]{{{3}\over{5}}} \\
&&\phantom{xxx}\blue{\text{both sides taken the }2 \text{-th root}}\\
x=\frac{1}{5}\sqrt{15} &\lor& x=-\frac{1}{5}\sqrt{15}\\
&&\phantom{xxx}\blue{\text{simplified}} \end{array}#

New example