Functies: Domein en bereik
 Domein
Domein
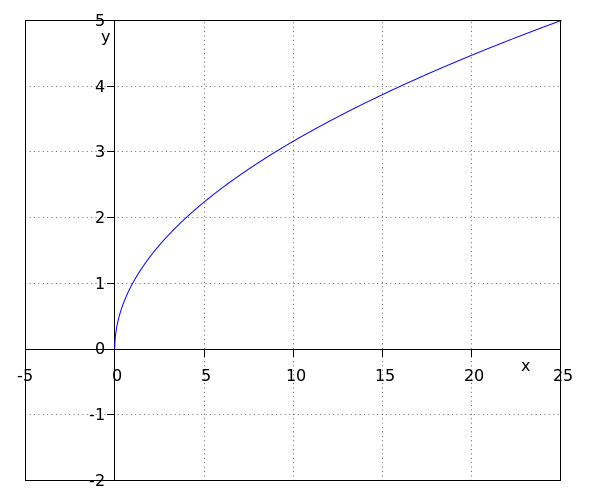
Bekijk de functie #f(x)=\sqrt{x}#.
In Wortels hebben we gezien dat de wortel van een negatief getal niet bestaat. Dat betekent dat we geen negatieve getallen voor #x# mogen substitueren in de functie #f#, omdat de functie dan niet bestaat.
Alle getallen #x# waarvoor #x \geq 0# kunnen we wel substitueren in #f#, dit zijn de getallen in het interval #\ivco{0}{\infty}#.
We zeggen dat het domein van #f# gelijk is aan het interval #[0,\infty)#.
Domein
Het domein van een functie #f# bestaat uit alle originelen van de functie.
Voorbeeld
Het domein van #f(x)=\sqrt{x-1}# is:
het interval #[1,\infty)#
Wat is het domein van de functie #f(x)=\frac{1}{x+1}#?
Ontgrendel volledige toegang


Toegang voor leraar
Vraag een demo account aan. Wij helpen je graag op weg met onze digitale leeromgeving.
Toegang voor student
Is jouw universiteit niet aangesloten?
Via Pass Your Math kan je toegang krijgen tot onze cursussen onafhankelijk van je onderwijsinstelling. Bekijk de prijzen en nog veel meer. Of ga naar
omptest.org als je een OMPT examen moet maken.
omptest.org als je een OMPT examen moet maken.



