Functies: Gebroken functies
Gebroken lineaire functies
Een gebroken lineaire functie is een functie van vorm
\[f(x)=\frac{\blue{a}x+\green{b}}{\purple{c}x+\orange{d}}\]
Hierin zijn #\blue{a}#, #\green{b}#, #\purple{c}# en #\orange{d}# getallen en is #x# een variabele.
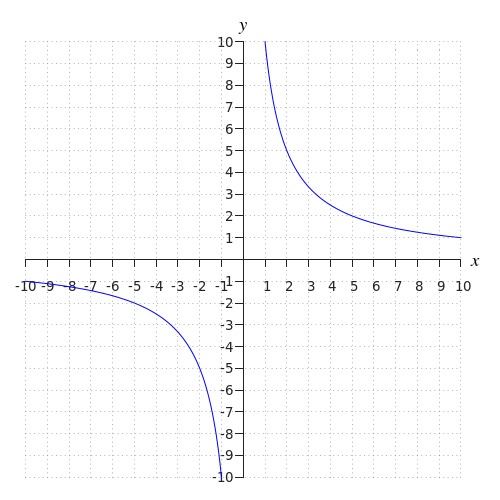
De grafiek van een gebroken lineaire functie is een hyperbool met een verticale en horizontale asymptoot.
We bepalen de verticale asymptoot van een gebroken lineaire functie #f(x)=\frac{\blue{a}x+\green{b}}{\purple{c}x+\orange{d}}# door de noemer #\purple{c}x+\orange{d}# gelijk aan #0# te stellen en deze vergelijking op te lossen.
Dus voor verticale asymptoot vinden we \[x=-\frac{\orange{d}}{\purple{c}}\]
De horizontale asymptoot bepalen we door te bedenken dat voor heel grote waarden van #x# de getallen #\green{b}# en #\orange{d}# te verwaarlozen zijn ten opzichte van de termen met #x#.
Dus krijgen we voor de horizontale asymptoot \[y=\frac{\blue{a}x}{\purple{c}x}=\frac{\blue{a}}{\purple{c}}\]
Bekijk de functie #f(x)=\frac{\blue{2}x+\green{-3}}{\purple{4}x+\orange{2}}#
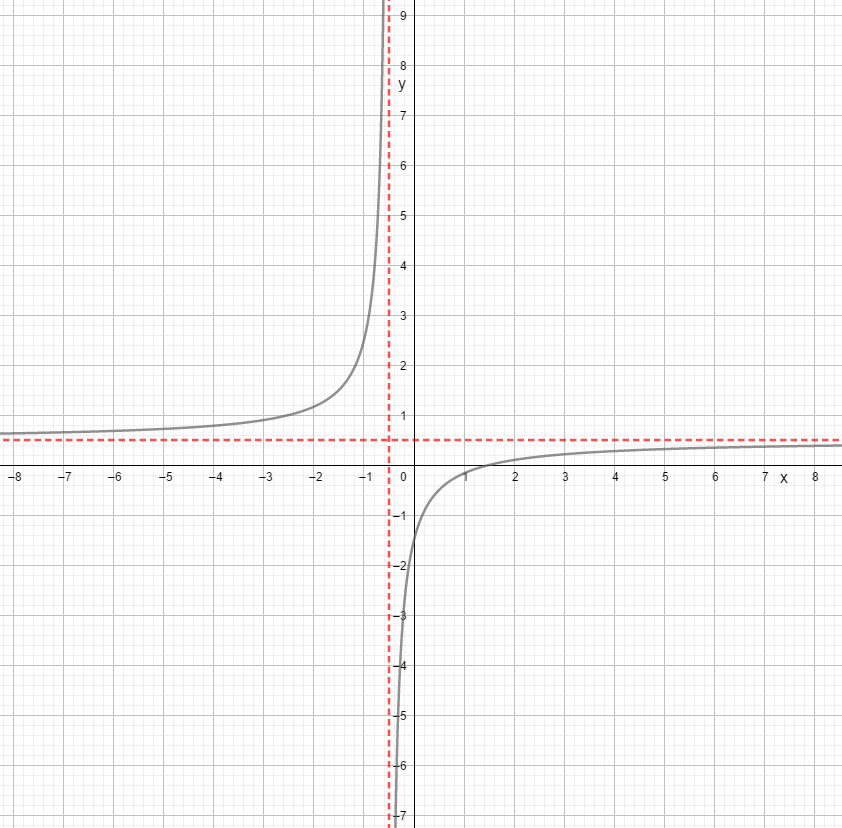
De verticale asymptoot is gelijk aan
\[x=-\frac{\orange{2}}{\purple{4}}=-\frac{1}{2}\]
De horizontale asymptoot is gelijk aan
\[y=\frac{\blue{2}}{\purple{4}}=\frac{1}{2}\]
omptest.org als je een OMPT examen moet maken.
