Basisbewerkingen met complexe getallen

Bewerkingen met complexe getallen: Rekenen met complexe getallen

Basisbewerkingen met complexe getallen

Net als bij alle andere getallen die we kennen, kunnen we algebraïsche bewerkingen uitvoeren met complexe getallen, zoals optelling, aftrekking, vermenigvuldiging en deling. Op deze pagina zullen we deze bewerkingen verkennen, waarbij we deling voor later bewaren. We beginnen met vermenigvuldiging met reële scalairen. Wanneer we een complex getal vermenigvuldigen met een reëel getal, verkrijgen we een nieuw complex getal.

Vermenigvuldiging met scalairen

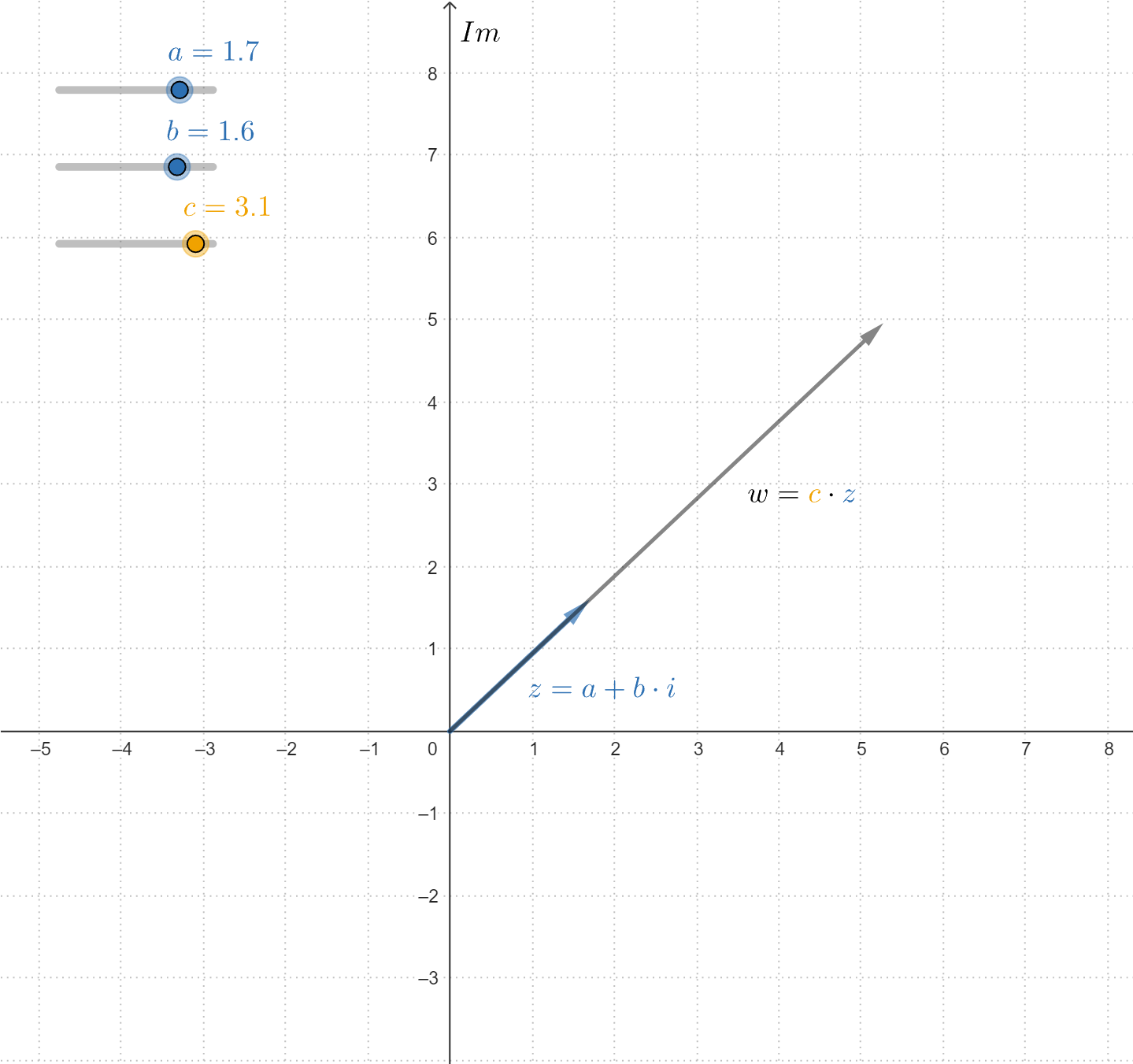
Laat #\blue{z}=\blue{a+b\cdot \complexi}# en #\orange{c}# een reëel getal zijn.

De vermenigvuldigingsbewerking met een scalair wordt gedefinieerd als
\[\begin{array}{rcl}
\orange{c}\cdot \blue{z} &=& \orange{c}\cdot \left(\blue{a+b\cdot \complexi}\right) \\
&=&\orange{c}\cdot \blue{a} + \orange{c}\cdot \blue{b}\cdot \blue{\complexi}
\end{array}\]

Visueel wordt dit weergegeven als een uitrekking of krimping van de vector in het arganddiagram.

Voorbeelden

\[\begin{array}{rcl}
\blue{z} &=& \blue{2 - \frac{1}{3} \cdot \ii} \\
\orange{3}\cdot \blue{z} &=& \orange{3} \cdot \blue{2} - \orange{3} \cdot \blue{\frac{1}{3} \cdot \ii}\\
&=& 6 - \ii \\
\orange{\frac{1}{2}}\cdot \blue{z} &=& \orange{\frac{1}{2}}\cdot \blue{2} - \orange{\frac{1}{2}}\cdot \blue{\frac{1}{3} \cdot \ii}\\
&=& 1 - \frac{1}{6} \cdot \ii \\
\end{array}\]

Visualisatie

Let op dat op deze manier elk component van #\blue{z}# wordt geschaald door #\orange{c}# en dat vermenigvuldiging met een scalair daarom voldoet aan de distributieve wet. Als we #\blue{z}# met een complex getal zouden vermenigvuldigen, zou het resultaat niet slechts een schaling van elke component zijn, zoals we later zullen zien.

Vervolgens behandelen we de optelling en aftrekking van complexe getallen. Wanneer we twee complexe getallen optellen (of aftrekken), worden de reële en imaginaire delen van het resultaat respectievelijk gegeven door de som (of aftrekking) van de reële en imaginaire delen van de oorspronkelijke getallen.

Optellen en aftrekken

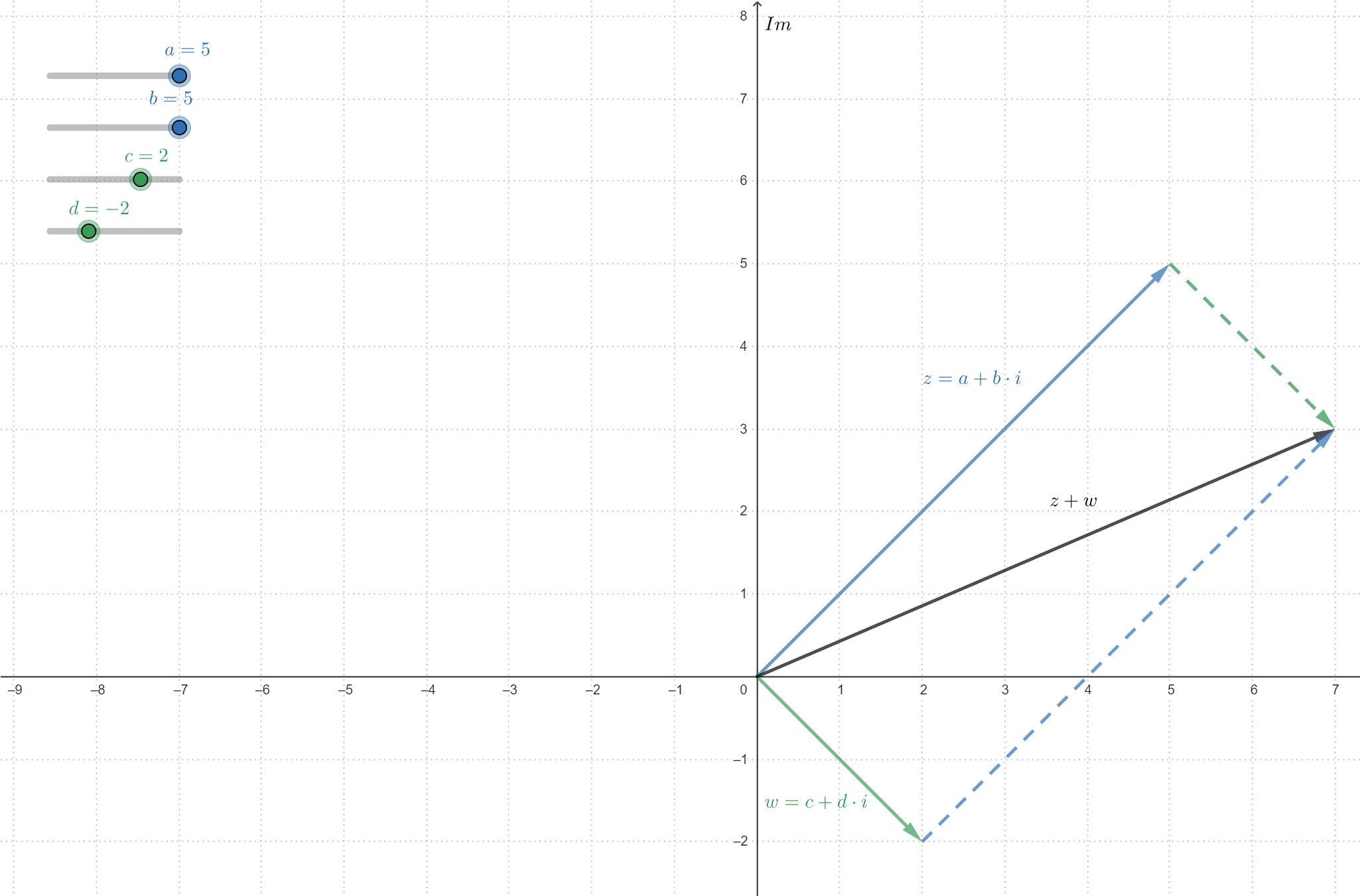
Laat #\blue{z}=\blue{a+b\cdot \complexi}# en #\green{w} = \green{c + d\cdot \complexi}#.

Hun optelling wordt gedefinieerd als

\[\begin{array}{rcl}
\blue{z} + \green{w} &=& \left(\blue{a+b\cdot \complexi}\right) + \left( \green{c + d\cdot \complexi}\right)\\ &=& \left(\blue{a} + \green{c}\right) + \left(\blue{b} + \green{d}\right)\cdot \complexi \end{array}\]

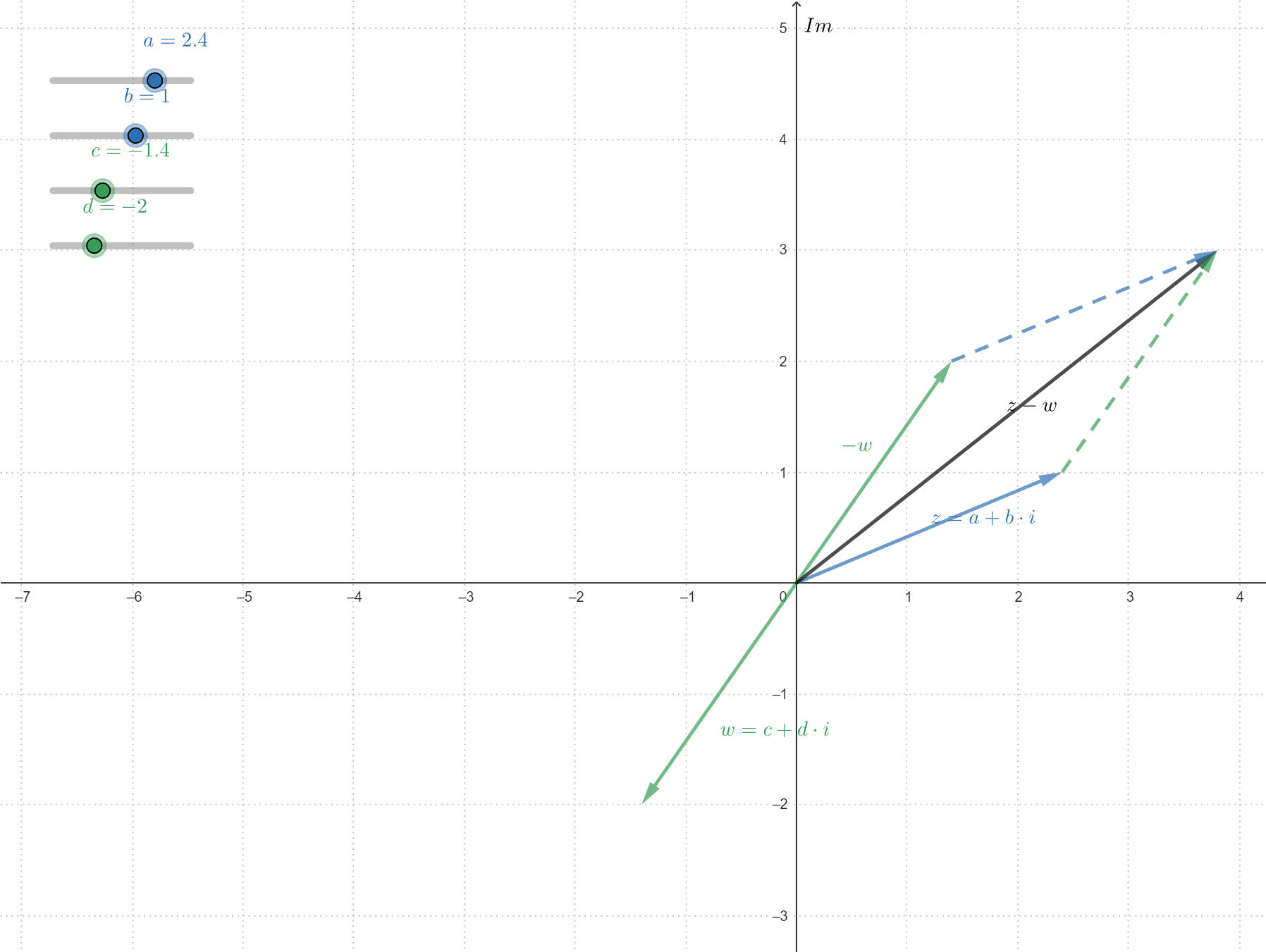
Hun aftrekking wordt gedefinieerd als

\[\begin{array}{rcl}
\blue{z} - \green{w} &=& \left(\blue{a+b\cdot \complexi}\right) - \left( \green{c + d\cdot \complexi}\right)\\ &=& \left(\blue{a} - \green{c}\right) + \left(\blue{b} - \green{d}\right)\cdot \complexi\end{array}\]

Voorbeelden

\[\begin{array}{rcl}
\blue{z} &=& \blue{2 - 5 \cdot \ii} \\
\green{w} &=& \green{-1 + 3 \cdot \ii} \\ \\
\blue{z}+\green{w} &=& (\blue{2}+(\green{-1})) + (\blue{-5}+\green{3}) \cdot \ii\\
&=& 1 -2 \cdot \ii \\ \\
\blue{z}-\green{w} &=& (\blue{2}-(\green{-1})) + (\blue{-5}-\green{3}) \cdot \ii\\
&=& 3 -8 \cdot \ii
\end{array}\]

In het Argand-diagram wordt de optelling van twee complexe getallen weergegeven door hun vectoren kop-staart te plaatsen, waarbij de resulterende vector de optelling voorstelt.

Opmerking

Merk op dat we hetzelfde resultaat #\blue{z}-\green{w}# zouden hebben gekregen als we in plaats daarvan #\green{w}# met #-1# hadden vermenigvuldigd en vervolgens het resultaat bij #\blue{z}# hadden opgeteld.

Visualisatie optellen

Visualisatie aftrekken

Nadat we de som en het verschil van complexe getallen hebben gedefinieerd en gevisualiseerd, laten we nu hun product behandelen. De vermenigvuldiging van complexe getallen volgt precies zoals we zouden verwachten van reële getallen. Zoals we in de blok laten zien, bevat het reële deel van het product van twee complexe getallen niet alleen het product van hun respectieve reële delen, maar ook het product van hun respectieve imaginaire delen.

Vermenigvuldiging van complexe getallen

Laat #\blue{z}=\blue{a + b\cdot \complexi}# en #\green{w} = \green{c + d\cdot \complexi}#. Dan wordt #\blue{z}\cdot \green{w}# gegeven door

\[\begin{array}{rcl}
\blue{z}\cdot \green{w} &=& \left(\blue{a+b\cdot \complexi}\right) \cdot \left(\green{c+d\cdot \complexi}\right) \\&=&\blue{a}\cdot \green{c} + \blue{a}\cdot \green{d}\cdot \complexi + \blue{b}\cdot\green{c}\cdot \complexi +\blue{b}\cdot\green{d}\cdot\left(\complexi^2\right)\\&=& \left(\blue{a}\cdot \green{c} - \blue{b}\cdot \green{d}\right) + \left(\blue{a}\cdot \green{d} + \blue{b}\cdot \green{c}\right)\cdot \complexi\end{array}\]

Voorbeeld

\[\begin{array}{rcl}
\blue{z} &=& \blue{2 + 4 \cdot \ii} \\
\green{w} &=& \green{1 + 3 \cdot \ii} \\ \\
\blue{z}\cdot \green{w} &=& \left(\blue{2}\cdot \green{1} - \blue{4}\cdot \green{3}\right) \\
&&\quad + \left(\blue{2}\cdot \green{3} + \blue{4}\cdot \green{1}\right)\cdot \ii \\
&=& -10+10 \cdot \ii
\end{array}\]

Machten van z

Net als bij reële getallen bestaan de machten van complexe getallen uit de herhaalde vermenigvuldiging van het getal met zichzelf. \[\blue{z}^{\orange{n}} = \underbrace{\blue{z}\cdot \blue{z}\cdot \blue{z}\cdot \ldots \cdot \blue{z}}_{\orange{n} \text{ times}}\]

Voorbeelden :
\[\begin{array}{rcl}\blue{z}^{\orange{2}} &=&\left(a + b\cdot \complexi\right)\cdot\left(a + b\cdot \complexi\right)\\
&=&a^2+2\cdot a\cdot b\cdot \complexi + b\cdot \complexi^2\\&=& a^2 + 2\cdot a\cdot b\cdot \complexi - b^2\\&&\\
\blue{z}^{\orange{3}} &=& \blue{z}\cdot \blue{z}^2\\
&=&\left(a+b\cdot \complexi\right) \cdot \left(a^2 +2\cdot a\cdot b\cdot \complexi - b^2 \right)\\
&=&a^3+2\cdot a^2\cdot b\cdot \complexi -b^2 \cdot a \\&&+\,b\cdot a^2\cdot \complexi + 2\cdot a\cdot b^2\cdot \complexi^2-b^3\cdot \complexi\\
&=& a^3 +3\cdot a^2\cdot b\cdot \complexi - 3\cdot a\cdot b^2 - b^3\cdot \complexi\end{array}\]

Zoals we kunnen zien, voldoet de vermenigvuldiging van complexe getallen aan dezelfde distributiewetten als die van reële getallen.

Schrijf de som van de twee complexe getallen \[-7+\complexi \qquad\text{en}\qquad 5-3\cdot \complexi\] in cartesische vorm.

#-2-2\cdot \complexi#

#\begin{array}{rcl}
(-7+\complexi) + (5-3\cdot \complexi) &=& (-7+5) + (1-3) \cdot \complexi \\
&&\qquad\blue{\text{gelijksoortige termen samengenomen}} \\
&=& -2-2\cdot \complexi \\
&&\qquad\blue{\text{vereenvoudigd}}
\end {array}#

Nieuw voorbeeld