Systems of linear equations and matrices: Conclusion of Systems of linear equations and matrices
Applications of systems of linear equations
We review some areas of application of systems of linear equations.
Stoichiometry of a chemical reaction The starting materials and end products of a chemical reaction are known, but in order to determine the quantities of the chemical substances in question, a chemical equation (the so-called stoichiometric equation) should be made to hold.
In combustion of methane \((\mathrm{CH}_4)\), water \((\mathrm{H}_2\mathrm{O})\) and carbon dioxide \((\mathrm{CO}_2)\) arise. In this case, it is not difficult to see that \[ \mathrm{CH}_4+2\mathrm{O}_2\longrightarrow 2\mathrm{H}_2\mathrm{O}+\mathrm{CO}_2\] is a balanced reaction in the sense that the same number of atoms of each type appears on both sides of equation.
For the less simple example of combustion of propane \((\mathrm{C}_3\mathrm{H}_8)\) it already helps to set up a system of linear equations and to ask for which values of \(p\), \(q\), \(r\), and \(s\) the chemical equation \[ p\mathrm{C}_3\mathrm{H}_8+q\mathrm{O}_2\longrightarrow r\mathrm{H}_2\mathrm{O}+s\mathrm{CO}_2\] is balanced. In this example, this leads to the equations \(3p=s\) , \(8p=2r\) and \(2q=r+2s\). The associated homogeneous set of linear equations is\[ \left\{\begin{array}{rrrrrrrrl} 3p & & & & &-& s & = & 0 \\ 8p & & & - & 2r & & & = & 0 \\ & & 2q & - & r & -& 2s & = & 0\end{array}\right. \] and the coefficient matrix is \[\left(\begin{array}{rrrr} 3 & 0 & 0 & -1\\ 8 & 0 & -2 & 0 \\ 0 & 2 & -1 & -2\\ \end{array}\right) \] The reduced echelon form of this matrix is equal to \[\left(\begin{array}{rrrr} 1 & 0 & 0 & -\frac{1}{3}\\ 0 & 1 & 0 & -\frac{5}{3} \\ 0 & 0 & 1 & -\frac{4}{3}\\ \end{array}\right) \] It follows that, for an arbitrarily chosen value of \(s\), the other values are determined by \[p=\frac{s}{3},\quad q=\frac{5s}{3},\quad r=\frac{4s}{3}\] In the chemical context, the stoichiometric coefficients must be non-negative integers; the smallest values with this property occur for \(s=3\), namely \(p=1\), \(q=5\), and \(r=4\). This leads to the following stoichiometric equation: \[ \mathrm{C}_3\mathrm{H}_8+5\mathrm{O}_2\longrightarrow 4\mathrm{H}_2\mathrm{O}+3\mathrm{CO}_2\]
Heating plate with an internal grid Consider a heating plate having an internal grid, as shown in the figure below. The temperatures of the plate at the boundary are constant and known.
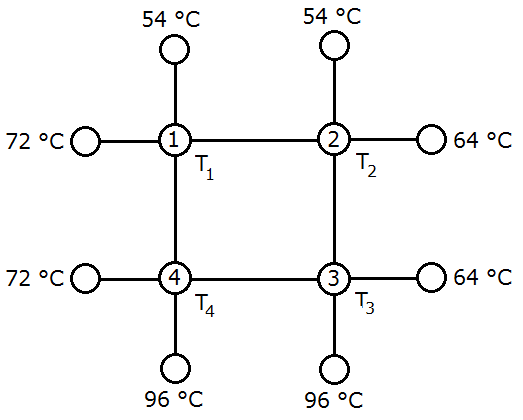
We assume that the temperature at a single node of the grid is the average of the four neighboring nodes (left, top, right, bottom). For example, for node #1# we have \(T_1=\tfrac{1}{4}(72+54+T_2+T_4)\), or \(4T_1=126+T_2+T_4\). To calculate the temperature of the internal nodes, we set up four equations with four unknowns by writing down this relation for every single node: \[ \left\{\begin{array}{rrrrrrrrl} 4T_1 & - & T_2 & & &-& T_4 & = & 126 \\ -T_1 & + & 4T_2 & - & T_3 & & & = & 118 \\ & - & T_2 & + & 4T_3 & -& T_4 & = & 160 \\ -T_1 & & & - & T_3 & + & 4T_4 & = & 168 \end{array}\right. \] The augmented matrix of the system of equations is \[\left(\begin{array}{rrrrr} 4 & -1 & 0 & -1 & 126 \\ -1 & 4 & -1 & 0 & 118 \\ 0 & -1 & 4 & -1 & 160 \\ -1 & 0 & -1 & 4 & 168 \end{array}\right) \] The reduced echelon form of this matrix is equal to \[\left(\begin{array}{rrrrr} 1 & 0 & 0 & 0 & \frac{269}{4} \\ 0 & 1 & 0 & 0 & \frac{261}{4} \\ 0 & 0 & 1 & 0 & \frac{303}{4}\\ 0 & 0 & 0 & 1 & \frac{311}{4}\end{array}\right) \] This means that the temperatures in degrees Celsius at the internal nodes equal \[T_1=\frac{269}{4},\quad T_2=\frac{261}{4},\quad T_3=\frac{303}{4},\quad T_4=\frac{311}{4}\]
Electrical network The figure below shows a network of electrical resistors, and a battery. In this figure, also the current intensities \(I_1,\ldots, I_7\) of the different components of the network are indicated.
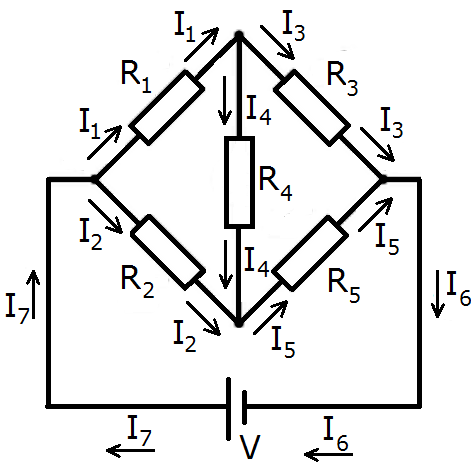With the three laws given below, we can calculate the currents as a function of the resistances \(R_1,\ldots, R_5\) and battery voltage \(V\).
Ohm's law The voltage #V# across a resistor #R# is proportional to the current intensity #I#: \[V=I\cdot R\]
Kirchhoff's voltage law The sum of the voltage differences in each closed loop of an electrical network is equal to zero.
Kirchhoff's current law At each node of an electrical network, the sum of the currents that come together at that point is equal to the sum of the currents that depart from that point.
Application of the first two laws gives the following equations \[ \left\{\begin{array}{rrrrrrl} R_1\cdot I_1 & + & R_4\cdot I_4 & - & R_2\cdot I_2 & = & 0 \\ R_4\cdot I_4 & + & R_5\cdot I_5 & - & R_3\cdot I_3 & = & 0 \\ R_2\cdot I_2 & + & R_5\cdot I_5 & - & V & = & 0\end{array}\right. \] Other loops can be ignored because they only produce equations that are linear combinations of the equations already given. Application of the third law gives the following equations \[ \left\{\begin{array}{rrrrr} I_1 & + & I_2 & = & I_7 \\ I_3 & + & I_4 & = & I_1 \\ I_2 & + & I_4 & = & I_5 \\ I_3 & + & I_5 & = & I_6\end{array}\right. \] We could also add the equation \(I_6=I_7\), but it is redundant with respect to the previous equations: \[I_6=I_3+I_5=I_3+I_4+I_2= I_1+I_2=I_7\] In short, we have 7 linear equations with 7 unknown currents \(I_1,\ldots, I_7\). The augmented matrix of the system of equations is \[\left(\begin{array}{rrrrrrrrr} R_1 & -R_2 & 0 & R_4 & 0 & 0 & 0 & 0 \\0 & 0 & -R_3 & R_4 & R_5 & 0 & 0 & 0 \\ 0 & R_2 & 0 & 0 & R_5 & 0 & 0 & V \\ 1 & 1 & 0 & 0 & 0 & 0 & -1 & 0 \\ -1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & -1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & -1 & 0 & 0 \end{array}\right) \] The reduced echelon form can be computed, and has a last column, which consists of rational expressions in the resistances \(R_1,\ldots, R_7\) and the battery voltage \(V\): \[\left(\begin{array}{rrrrrrrrr} 1 & 0 & 0 & 0 & 0 & 0 & 0 & (R_2R_3+R_2R_4+R_2R_5+R_4R_5)\cdot V/N \\0 & 1 & 0 & 0 & 0 & 0 & 0 & (R_1R_3+R_1R_4+R_1R_5+R_3R_4)\cdot V/N \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & (R_1R_5+R_2R_4+R_2R_5+R_4R_5)\cdot V/N \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & (R_2R_3-R_1R5)\cdot V/N \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & (R_1R_3+R_1R_4+R_2R_3+R_3R_4)\cdot V/N \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & T \cdot V/N \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & T \cdot V/N \end{array}\right) \] with factor \(T\) and denominator \(N\) given by \[\begin{array}{rrl} T & = & R_1R_3+R_1R_4+R_1R_5+R_2R_3+{}\\ & & R_2R_4+R_2R_5+R_3R_4+R_4R_5 \\ N & = & R_1R_2R_3+R_1R_2R_4+R_1R_2R_5+R_1R_3R_5+{}\\ & & R_1R_4R_5+R_2R_3R_4+R_2R_3R_5+R_3R_4R_5\end{array}\] For the current intensity #I_4# on the "bridge" of the network we have \[I_4=\frac{(R_2R_3-R_1R_5)V}{N}\] This current does not depend on the resistance \(R_4\) and is (for #V\ne0#) equal to zero if and only if \( \displaystyle \frac{R_1}{R_2} = \frac{R_3}{R_5}\), that is to say, if the proportions \(R_1:R_2\) and \(R_3:R_5\) are equal to each other.
Word problems and mathematical puzzles Puzzles can often be translated into systems of linear equations.
Puzzle about ages The following is known about the ages of Kevin, Leo, and Michael:
- Currently, Kevin is two years younger than Leo and Michael together.
- In three years, Kevin will be twice as old as Leo.
- Two years ago, Leo was half as old as Michael.
How old are Kevin, Leo, and Michael?
Suppose that \(K\), \(L\), and \(M\) are the unknown ages of Charles, Leo, and Michael, respectively. We translate the three facts into the following three linear equations \[ \lineqs{K &=& L+M - 2 \cr K + 3 &=& 2\,(L+3) \cr L - 2 &=& \frac{1}{2}(M-2)}\] Equivalent this system is \[ \left\{\begin{array}{rrrrrrrl} K & - & L & - & M & = & -2 \\ K & - & 2L & & & = & 3 \\ & & 2L & - & M & = & 2 \end{array}\right. \] The reduced echelon form of the corresponding augmented matrix is \[\left(\begin{array}{rrrr} 1 & 0 & 0 & 17 \\ 0 & 1 & 0 & 7\\ 0 & 0 & 1 & 12 \end{array}\right) \] So the respective ages of Kevin, Leo, and Michael are #17#, #7#, and #12# years.
Puzzle about numbers, We assume that a natural number consists of two digits (in the decimal system) and that it has the following properties:
- the sum of the digits is #11#;
- when you reverse the digits in the number, you get a larger number that differs by #45# from the original number.
What number are we talking about?
Suppose that the number we are looking for is equal to \(10t+e\), where the variable \(t\) stands for the number of multiples of ten (the first digit), and \(e\) for units (the second digit). Then, we can translate the two data to the following two linear equations \[ \lineqs{t+e &=& 11 \cr 10e + t &=& 10t+e+45}\] Equivalent to this system is \[ \left\{\begin{array}{rrrrl} t & + & e & = & 11 \\ -9t & + & 9e & = & 45 \end{array}\right. \] The reduced echelon form of the associated augmented matrix is \[\left(\begin{array}{rrr} 1 & 0 & 3 \\ 0 & 1 & 8 \end{array}\right) \] So \(t=3\) and \(e=8\). Therefore, the number we are looking for is equal to \(38\).
Graphs of functions specified points Suppose we have three points \(\rv{-4,3}\) , \(\rv{3,3}\) and \(\rv{5,6}\) in the plane, and we want to determine the equation of the parabola through these points. We can solve this problem through a system of linear equations.
First, we write the general equation for the parabola in the form \(y=ax^2+bx+c\). If we view this equation as a function rule, then it follows from \(y(-4)=3\), \(y(3)=3\), and \(y(5)=6\) that we have the following system of linear equations with unknowns \(a\), \(b\), and \(c\): \[ \left\{\begin{array}{rrrrrrrl} 16a & - & 4b & + & c & = & 3 \\ 9a & + & 3b & + & c & = & 3 \\ 25a & + & 5b & + & c & = & 6 \end{array}\right. \] The augmented matrix of this system of equations is \[\left(\begin{array}{rrrr} 16 & -4 & 1 & 3 \\ 9 & 3 & 1 & 3 \\ 25 & 5 & 1 & 6 \end{array}\right) \] The reduced echelon form of this matrix is equal to \[\left(\begin{array}{cccc} 1 & 0 & 0 & \frac{1}{6} \\ 0 & 1 & 0 & \frac{1}{6} \\ 0 & 0 & 1 & 1 \end{array}\right) \] This means that \(a=\frac{1}{6}\) , \(b=\frac{1}{6}\) and \(c=1\), in other words: the equation of the required parabola is equal to \[y=\frac{1}{6}x^2+\frac{1}{6}x+1\]
Magic triangles and squares People have always been fascinated by magic numbers triangles, squares, cubes, etc. We will deal with magic triangles and magic squares.
Magic triangles The triangle\[\begin{array}{ccccc} & & a & & \\ & b & & f & \\ c & & d & & e\end{array}\] of numbers where \(a, b,\ldots,f\) are integers, is called magical if the sum of all the numbers on each side is the same. For example, the numbers triangle \[\begin{array}{ccccc} & & -1 & & \\ & 6 & & 4 & \\ 1 & & 2 & & 3\end{array}\] is magical because the sum of all the numbers on each side is equal to six. The question of finding all the magical triangles is equivalent to solving the following two equations in six unknowns: \[ \left\{\begin{array}{c}a+b+c = c+d+e \\ a+b+c = a+f+e \end{array}\right. \] which can be simplified directly to \[ \left\{\begin{array}{c}a+b=d+e \\ b+c = f+e \end{array}\right. \] From \(a+b=d+e\) and \(b+c=f+e\) it then follows that \(b=f+e-c\) and \(a=d+e-b=d+c-f\). In other words, all the magic triangles are of the form \[\begin{array}{ccccc} & & d+c-f & & \\ & f+e-c & & \phantom{d+}f\phantom{-c} & \\ c & & d & & e\end{array}\] where \(c, d, e, f\) can be freely chosen. Then the sum of the numbers on each side is equal to #c+d+e#.
Magic Squares Now we look at magic squares of size \(3\times 3\), that is squares of integers for which the sum of the three numbers on each side and each diagonal is the same. The general form of a magic square of dimension \(3\times 3\) is \[\begin{array}{ccc} x_1 & x_2 & x_3 \\ x_4 & x_5 & x_6 \\ x_7 & x_8 & x_9 \end{array}\] where the defining property leads to the following system of seven linear equations in nine unknowns \[ \left\{\begin{array}{c} x_1+x_2+x_3 = x_4+x_5+x_6 \\ x_4+x_5+x_6 = x_7+x_8+x_9 \\ x_1+x_2+x_3 = x_1+x_4+x_7 \\ x_1+x_4+x_7 = x_2+x_5+x_8 \\ x_2+x_5+x_8 = x_3+x_6+x_9 \\ x_1+x_2+x_3 = x_1+x_5+x_9 \\ x_1+x_5+x_9 = x_3+x_5+x_7 \end{array}\right. \] Gaussian elimination results in the following reduced echelon form of the coefficient matrix associated with the system of equations \[\left(\begin{array}{rrrrrrrrr} 1 & 0 & 0 & 0 & 0 & 0 & -\frac{2}{3} & -\frac{2}{3}& \frac{1}{3}\\ 0 & 1 & 0 & 0 & 0 & 0 & -\frac{2}{3} & \frac{1}{3}& -\frac{2}{3}\\ 0 & 0 & 1 & 0 & 0 & 0 & \frac{1}{3} & -\frac{2}{3}& -\frac{2}{3}\\ 0 & 0 & 0 & 1 & 0 & 0 & \frac{2}{3} & -\frac{1}{3}& -\frac{4}{3}\\ 0 & 0 & 0 & 0 & 1 & 0 & -\frac{1}{3} & -\frac{1}{3}& -\frac{1}{3}\\ 0 & 0 & 0 & 0 & 0 & 1 & -\frac{4}{3} & -\frac{1}{3}& \frac{2}{3}\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right)\] The general form of a magic square is therefore \[\begin{array}{ccc} \frac{2p+2q-r}{3} & \frac{2p-q+2r}{3} & \frac{-p+2q+2r}{3} \\ \frac{-2p+q+4r}{3} & \frac{p+q+r}{3} & \frac{4p+q-2r}{3} \\ p & q & r \end{array}\] where \(p\), \(q\), and \(r\) are numbers that can be chosen freely under the condition that no fractions appear in the square after simplification. This condition is automatically fulfilled by the choice #p=a+b#, #q=a-b-c#, and #r=a+c# where \(a\), \(b\), and \(c\) are integers that can be chosen freely. The above general form of a magic square is then explicitly free of fractions: \[\begin{array}{ccc} a-c & a+b+c & a-b \\ a-b+c & a & a+b-c \\ a+b & a-b-c & a+c \end{array}\] The sum of the three numbers on each side and each diagonal is always equal to #3a#.
The famous magic square, where each of the numbers \(1,\ldots, 9\) is used exactly once, is called Lo Shu and arises at the parameter choice \(a=5, b=3, c=1\): \[\begin{array}{ccc} 4 & 9 & 2 \\ 3 & 5 & 7 \\ 8 & 1 & 6 \end{array}\]
Or visit omptest.org if jou are taking an OMPT exam.
