Just as a line is described in the plane by an equation in two unknowns, a plane in three-dimensional space is described by an equation in three unknowns:
Let \(a\), \(b\), \(c\), and \(d\) be real numbers. The solution of the equation \[a\cdot x+b\cdot y+c\cdot z+d=0\] with unknown #x#, #y#, and #z#, can be seen as a collection of points in three-dimensional space: it consists of all points \(\rv{x,y,z}\) that satisfy the above equation. If at least one of #a#, #b#, #c# is distinct from #0#, then the solution is a plane.
- If \(c\ne0\), then we can write the equation as \(z=-\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}\). After all, this is the solution if we regard \(x\) and \(y\) as parameters and \(z\) as unknown. It indicates that for each value of \(x\) and \(y\), there is a point \(\rv{x,y,z}\) with \(z\) equal to \(-\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}\).
- If \(a \ne 0\) or \(b \ne 0\), then we have an inclined plane.
- If \(a=0\) and \(b=0\), then the value of \(z\) is always equal to \(-\frac{d}{c}\), and we have a horizontal plane.
- In the exceptional case \(c=0\), the equation looks like \(a\cdot x+b\cdot y+d=0\).
- If \(a \ne 0\) or \(b \ne 0\), then we have a vertical plane.
- If \(a=0\) and \(b=0\) and
- \(d\ne 0\), then there are no solutions;
- \(d=0\), then any triplet of values of \(x\), \(y\), and \(z\) is a solution.
An inclined plane is the graph of the function \(z(x,y)=-\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}\). A vertical plane is the graph of the function \(x(y,z) = -\frac{b}{a}y-\frac{c}{a}z-\frac{d}{a}\) if #a\ne0# and of the function \(y(x,z) = -\frac{a}{b}x-\frac{c}{b}z-\frac{d}{b}\) if #b\ne0#.
We speak of an equation of a plane because more equations are possible: for each number \(k\ne 0\), the equations \(a\cdot x+b\cdot y+c\cdot z+d=0\) and \((k\cdot a)x+(k\cdot b)y+(k\cdot c)z+(k\cdot d)=0\) describe the same plane.
Conversely, each pair of linear equations in #x#, #y#, #z# that describe the same plane is equal up to a constant multiple.
In terms of the dot product #{\vec{u}}\boldsymbol{\cdot}{\vec{v}}=u_1\cdot v_1+u_2\cdot v_2+u_3\cdot v_3#, we can write the equation as
\[\rv{a,b,c}\boldsymbol{\cdot}\rv{x,y,z}=-d\]
As a consequence, #\rv{a,b,c} # is perpendicular to each direction vector of the plane. Therefore, this vector called a normal vector of the plane. The normal vector is uniquely determined up to a scalar multiple.
By describing planes in terms of equations, we are able to find points of intersection of planes as solutions of systems of linear equations.
The intersection of planes (that is, the set of points they have in common intersection) which are described by linear equations in the coordinates #x#, #y#, #z#, can be found by solving the system consisting all of the equations corresponding to these planes.
The intersection of two planes that are not parallel, is a line and can be described with the aid of a single parameter.
If several different planes have a common pont of intersection, then their intersection is a point or a line.
A line can be described by two linear equations, which belong to different planes. Those planes are not uniquely determined: each pair of planes containing the line is associated with a pair of equations describing the line (that is to say, the solution of which is the line).
Planes are parallel if and only if they have the same normal vectors. Two planes do not have any points of intersection in that case alone.
It is possible that three non-parallel planes have no common intersection points. An example is given below.
Also, an equation of the plane passing through three different points can be found by solving a system of linear equations:
Suppose that three distinct points in \(\mathbb{R}^3\) are represented by the vectors \(\vec{p}=\rv{p_1,p_2,p_3}\), \(\vec{q}=\rv{q_1,q_2,q_3}\) and \(\vec{r}=\rv{r_1,r_2,r_3}\). Then, each plane passing through these three points \(\vec{p}\), \(\vec{q}\), and \(\vec{r}\) has a linear equation of the form
\[a\cdot x+b\cdot y+c\cdot z+d=0\] where #\rv{a, b, c,d}# is a solution distinct from #\rv{0,0,0,0}# of the system of linear equations
\[\eqs{ p_1\cdot a+ p_2\cdot b+ p_3\cdot c+d &=&0\\ q_1\cdot a+ q_2\cdot b+ q_3\cdot c+d &=&0\\ r_1\cdot a+ r_2\cdot b+ r_3\cdot c+d &=&0\\ }\]
If the three points \(\vec{p}\), \(\vec{q}\), and \(\vec{r}\) lie on one line, then there are more planes that satisfy the conditions. If not, then there is exactly one such plane, and the coefficients #a#, #b#, #c#, #d# of the equation of the plane are uniquely determined up to a scalar multiple.
The plane passing through three points #\vec{p}#, #\vec{q}#, and #\vec{r}# has an equation of the form \[a\cdot x+b\cdot y+c\cdot z + d=0\] for certain numbers #a#, #b#, #c#, #d# with at least one of #a#, #b#, #c# distinct from #0#. The three equations of the theorem express the fact that #\vec{p}#, #\vec{q}#, and #\vec{r}# must be solutions of the equation.
Note that #\rv{a,b,c,d}=\rv{0,0,0,0}# indeed imlpies that at least one of #a#, #b#, #c# is distinct from #0#, because if #a=b=c=0#, then the given equations force that #d=0#.
The constant term #d# can be made to disappear from the equations by subtracting one equation from another. By means of the dot product, the resulting equations can be written as \[\rv{a,b,c}\boldsymbol{\cdot}\left(\vec{p}-\vec{q}\right)=0\] for the equations involving #\vec{p}# and #\vec{q}#, and similarly for the other pairs of points. The normal vector #\rv{a,b,c}# can be found as a solution of these equations.
The linear equation can be written explicitly:
\[ \begin{array}{rcl}\left( -{q_2}\,{r_3}+{p_2}\,{r_3}+{q_3}\,
{r_2}-{p_3}\,{r_2}-{p_2}\,{q_3}+{p_3}\,
{q_2} \right)\cdot x &&\\ + \left({q_1}\,{r_3}-\,{p_1}\,{r_3}-\,
{q_3}\,{r_1}+\,{p_3}\,{r_1}+\,{p_1}\,{q_3}
-\,{p_3}\,{q_1}\right) \cdot y&&\\ +\left(-{q_1}\,{r_2}+\,{p_1}\,
{r_2}+\,{q_2}\,{r_1}-\,{p_2}\,{r_1}-\,
{p_1}\,{q_2}+\,{p_2}\,{q_1}\right) \cdot z&& \\ + \left({p_1}\,
{q_2}\,{r_3}-\,{p_2}\,{q_1}\,{r_3}-\,{p_1}
\,{q_3}\,{r_2}+\,{p_3}\,{q_1}\,{r_2}+\,
{p_2}\,{q_3}\,{r_1}-\,{p_3}\,{q_2}\,{r_1}
\right) &=&0\end{array} \]
However, it is more convenient to solve the system of linear equations using standard techniques than to memorize this formula.
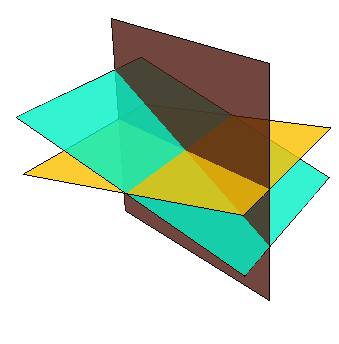
Given are the three planes:
\[\begin{array}{rcl} U &:\quad &x+2y=0\\ V &:\quad & x+2z=0\\ W&:\quad & z=0\end{array}\]
Determine the intersection of the three planes #U#, #V#, and #W#.
The three planes #U#, #V#, and #W# intersect each other at the point \(\rv{0,0,0}\).
This can be seen by first substituting #z=0# (the value determined by the third equation) in the other two equations, and next substituting #x=0# (the value determined by the new second equation), and concluding that the first equation now forces #y=0#.
The three planes are shown in the figure below.
 Planes in space
Planes in space





