For an indication of the origin of the concept of inner product, we look at the plane.
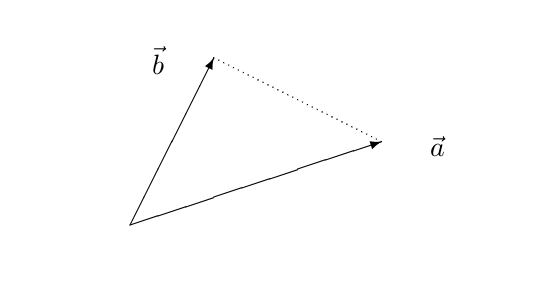
In the plane, a triangle two of whose sides correspond to the vectors #\vec{a}# and #\vec{b}#, the third side has length #\parallel \vec{a}-\vec{b}\parallel#. If the angle between the vectors #\vec{a}# and #\vec{b}# is equal to #\varphi#, then the law of cosines tells us that
\[ \norm{\vec{a}-\vec{b}}^2 =\norm{\vec{a}}^2 +
\norm{\vec{b}}^2 -2\,\norm{\vec{a}}\cdot\norm{\vec{b}}\cdot
\cos(\varphi)
\] The term #\norm{\vec{a}}\cdot\norm{\vec{b}}\cdot\cos(\varphi)# on the right-hand side is the inner product of two vectors #\vec{a}# and #\vec{b}# in the plane. For #\vec{a}=\vec{b}#, this term gives the square of the length of #\vec{a}#. The angle between two vectors is also built into this inner product. In the theory of inner products in abstract vector spaces, we cannot start with such an explicit formula nor do we have a definition of length, so the above expression does not make sense. Therefore, we start from certain properties that this inner product on the plane appears to have: symmetry in the two arguments #\vec{a}# and #\vec{b}#, linearity in each of the arguments #\vec{a}# and #\vec{b}# separately, and positivity of the expression if #\vec{a}=\vec{b}\ne\vec{0}#. This gives us a hold on the definition of inner product for abstract vector spaces.
Let #V# be a real vector space. An inner product on #V# is a function that assigns to every pair of vectors #\vec{a},\vec{b}# from #V# a real number #\dotprod{\vec{a}}{\vec{b}}# in such a way that the following three properties are satisfied.
- bilinearity: #\dotprod{\vec{a}}{\vec{b}}# is linear in both #\vec{a}# and #\vec{b}#:
\[\begin{array}{rcl}
\dotprod{(\lambda \vec{v}+\mu \vec{w})}{\vec{b}}&= &\lambda \cdot(\dotprod{\vec{v}}{\vec{b}})+\mu\cdot (\dotprod{\vec{w}}{\vec{b}})\\
\dotprod{\vec{a} }{(\lambda \vec{v}+\mu \vec{w})} & =&\lambda\cdot (\dotprod{\vec{a}}{ \vec{v}})+\mu \cdot(\dotprod{\vec{a}}{\vec{w}})
\end{array}
\] for all scalars and vectors;
- symmetry: #\dotprod{\vec{a}}{\vec{b}} = \dotprod{\vec{b}}{\vec{a}}# for all #\vec{a},\vec{b}\in V#;
- positive-definiteness: #\dotprod{\vec{a}}{\vec{a}}\geq 0# for all #\vec{a}\in V#, and #\dotprod{\vec{a}}{\vec{a}} = 0# if and only if #\vec{a}= \vec{0}#.
A real vector space with an inner product is often referred to as a (real) inner product space.
An inner product is also called dot product. This name is suggested by the notation #\dotprod{\vec{a}}{\vec{b}}#.
The definition of inner product on complex vector spaces is slightly different. This is treated elsewhere.
On #\mathbb{R}^n# we can define an inner product in many ways. The following inner product is used very often; it is called the standard inner product. If #\vec{a}\ = \rv{a_1,a_2,\ldots,a_n}# and #\vec{b}\ = \rv{b_1,b_2,\ldots,b_n}# are vectors of #\mathbb{R}^n#, then
\[\dotprod{\vec{a}}{\vec{b}}\ = \ a_1\cdot {{b}_1}+a_2\cdot {{b}_2}+\cdots +a_n \cdot{{b}_n}
\]It is straightforward to check the requirements of an inner product for the standard inner product.
If we refer to #\mathbb{R}^n# as an inner product space without mentioning a specific inner product, we mean that the inner product is the standard inner product.
Another way of expressing the standard inner product in terms of column vectors #\vec{a}# and #\vec{b}# is
\[\dotprod{\vec{a}}{\vec{b}}\ = \vec{a}^\top\, \vec{b}\]
Let #V# be the set of continuous real functions defined on an interval #\ivcc{a}{b}#. Then #V# with the usual pointwise addition and scalar multiplication is a vector space. Take #f,g\in V# and define
\[ \dotprod{f}{g} = \int_a^b f(x)\cdot {g(x)}\,\dd x
\]This is an inner product on #V#. The bilinearity and the symmetry are easily checked. The third property can be proven as follows. Take a function #f# in #V# and suppose that this function is not equal to the zero function. Then there is a number #\alpha# in the interval #\ivcc{a}{b}# such that #f(\alpha)\neq 0#. Due to the continuity of #f# there is an open interval around #\alpha# with the property that #|f(x)|\gt \frac{1}{2}\cdot |f(\alpha)|\gt 0# for all #x# in that interval. Let #\delta# be the length of this interval. Then, by restricting the integral to the interval around #\alpha#, we have
\[
\dotprod{f}{f} = \int_a^b f(x)^2\dd x\geq \frac14\delta\cdot f(\alpha )^2\gt 0
\] So if #\dotprod{f}{f} = \ 0#, then necessarily #f(x) = 0# for all #x\in\ivcc{a}{b}#.
By symmetry we need only demand linearity in #\vec{a}#; linearity in #\vec{b}#, and so bilinearity, then follows automatically.
The value #0# is not only attained at #\vec{a}=\vec{b}=\vec{0}#, but also if one of the two arguments equals #\vec{0}#:
\[\dotprod{\vec{a}}{\vec{0}} = \dotprod{\vec{0}}{\vec{b}} = 0\] This follows from the bilinearity of the inner product. However, there are also cases in which the two vectors are not equal to #\vec{0}# but the inner product does equal #0#. For example, consider the inner product of the vectors #\rv{0,1}# and #\rv{1,0}# in the vector space #\mathbb{R}^2# with respect to the standard inner product. If two vectors have inner product #0#, these vectors are called orthogonal or perpendicular. Later we will elaborate on it.
Since, for each vector #\vec{a}# in an inner product space, #\dotprod{\vec{a}}{\vec{a}}# is a non-negative real number, the expression #\sqrt{\dotprod{\vec{a}}{\vec{a}}}# is well defined. We use it to define length:
In an inner product space the length or norm of a vector #\vec{a}# is defined by
\[ \norm{\vec{a}}=\sqrt{\dotprod{\vec{a}}{\vec{a}}} \] The distance between the vectors #\vec{a}# and #\vec{b}# is defined as the length of the difference vector #\vec{a}-\vec{b}#, that is to say, #\norm{\vec{a} -\vec{b}}#.
The length of #\rv{1,1,1,1}\in \mathbb{R}^4# with respect to the standard inner product is equal to
\[
\sqrt{1^2+1^2+1^2+1^2}=\sqrt{4}=2
\] The distance between #\rv{2,1,3,4}# and #\rv{5,1,7,4}# is
\[
\sqrt{(2-5)^2 + (1-1)^2 + (3-7)^2 + (4-4)^2}=\sqrt{9+16}=5\]
In the inner product space #V# with the above inner product of functions on the interval #\ivcc{a}{b} = \ivcc{0}{1}# the length of the function #f(x) = x^2# is equal to
\[
\norm{f}= \sqrt{\int_0^1 x^2 \cdot x^2 \, \dd x}=\sqrt{\left[\frac15 x^5\right]_0^1}=\frac{1}{5}\, \sqrt{5}
\]
In general, a function #d(\vec{a},\vec{b})# of the two variables #\vec{a}# and #\vec{b}# from the same vector space is called a distance function, if the following three properties hold for all vectors #\vec{a}#, #\vec{b}#, and #\vec{c}#:
- positivity: #d(\vec{a},\vec{b}) \ge 0# with equality if and only if #\vec{a}=\vec{b}#
- symmetry: #d(\vec{a},\vec{b}) =d(\vec{b},\vec{a}) #
- triangle inequality: #d(\vec{a},\vec{c})\le d(\vec{a},\vec{b}) + d(\vec{b},\vec{c}) #
The function #d(\vec{a},\vec{b})=\parallel\vec{a}-\vec{b}\parallel # is a distance function: the positivity results from the positivity of the inner product. The symmetry is clear from the bilinearity of the inner product: \[\begin{array}{rcl}d(\vec{b},\vec{a})&=&\norm{\vec{b}-\vec{a}}\\ &=&\norm{-(\vec{a}-\vec{b})}\\&=&\sqrt{\dotprod{(-(\vec{a}-\vec{b}))}{(-(\vec{a}-\vec{b}))}}\\&=&\sqrt{(-1)^2\cdot \dotprod{(\vec{a}-\vec{b})}{(\vec{a}-\vec{b})}}\\ & =&\norm{\vec{a}-\vec{b}}\\ &=&d(\vec{a},\vec{b}) \end{array}\] The triangle inequality will be proven later.
Later we will prove that the norm has the following interesting features. Here, #\vec{v}# is a vector of an inner product space #V# and #\lambda# is a scalar.
- #\norm{\lambda\vec{v}}= \abs{\lambda} \,\cdot \norm{\vec{v}}#
- #\norm{\vec{v}}\ge0#
- #\norm{\vec{v}}=0# if and only if #\vec{v}=0#
The formula below shows that an inner product is uniquely determined by the length.
In an inner product space, the following formula holds for all vectors #\vec{a}# and #\vec{b}#.
\[ \dotprod{\vec{a} }{\vec{b}}=\frac12\left(\norm{\vec{a}+\vec{b}}^2-\norm{\vec{a}}^2-\norm{\vec{b}}^2 \right)\]
We start elaborating the right-hand side and arrive at the left-hand side:
\[\begin{array}{rcl}\dfrac12\left(\norm{\vec{a}+\vec{b}}^2-\norm{\vec{a}}^2-\norm{\vec{b}}^2 \right) &=&\dfrac12\left(\dotprod{(\vec{a} +\vec{b}) }{(\vec{a} +\vec{b})}-\dotprod{\vec{a} }{\vec{a} }-\dotprod{\vec{b} }{\vec{b} } \right) \\&&\phantom{xxx}\color{blue}{\text{definition of length}}\\&=&\dfrac12\left(\left(\dotprod{\vec{a}}{\vec{a}} +\dotprod{\vec{a}}{\vec{b} }+\dotprod{\vec{b} }{\vec{a}}+\dotprod{\vec{b}}{\vec{b}}\right)-\dotprod{\vec{a} }{\vec{a} }-\dotprod{\vec{b} }{\vec{b} } \right) \\&&\phantom{xxx}\color{blue}{\text{bilinearity of the inner product}}\\&=&\dfrac12\left(\dotprod{\vec{a}}{\vec{b}} +\dotprod{\vec{b} }{\vec{a}}\right) \\ &&\phantom{xxx}\color{blue}{\text{simplified}}\\&=&\dfrac{1}{2}\left(\dotprod{\vec{a}}{\vec{b}}+\dotprod{\vec{a}}{\vec{b}}\right)\\ &&\phantom{xxx}\color{blue}{\text{symmetry of the inner product}}\\ &=&\dotprod{\vec{a} }{\vec{b} }\\ &&\phantom{xxx}\color{blue}{\text{simplified}}\\ \end{array}\]
Consider the vector space #\mathbb{R}^3# with standard inner product.
What is the inner product of the vectors #\vec{x}=\rv{1,0,1}# and #\vec{y}=\rv{5,-1,-1}#?
#4#
The value of the inner product can be found as follows:
\[\begin{array}{rcl}
\dotprod{\vec{x}}{\vec{y}}&=&\dotprod{\rv{1,0,1}}{\rv{5,-1,-1}}\\
&&\phantom{xx}\color{blue}{\text{vectors written out}}\\
&=&1\cdot 5+0\cdot(-1)+1\cdot (-1)\\
&&\phantom{xx}\color{blue}{\text{definition of standard inner product}}\\
&=&4\\
&&\phantom{xx}\color{blue}{\text{simplified}}
\end{array}\]
 Inner products on real vector spaces
Inner products on real vector spaces





