Vectorrekening in vlak en ruimte: Het uitproduct
 Uitproduct in 3 dimensies
Uitproduct in 3 dimensies
Zoals we weten is het inproduct van twee vectoren een getal, evenals het uitproduct in twee dimensies. In drie dimensies is er ook een uitproduct. Het levert bij twee vectoren in de ruimte een vector af met bijzondere eigenschappen. Het gaat hierbij om een vector die loodrecht op de twee gegeven vectoren staat, maar daarbij is een oriëntatie nodig: een regel die je vertelt welke kant het uitproduct op wijst. Daarom leggen we eerst een oriëntatie vast.
Rechtshandige oriëntatie
Drie vectoren #\vec{v}#, #\vec{w}#, #\vec{u}# (in deze volgorde) die een basis van de ruimte zijn, heten rechtshandig georiënteerd als #\vec{u}# aan de kant van het vlak door #\vec{0}#, #\vec{v}#, #\vec{w}# ligt die als volgt door de middelvinger aangewezen wordt: als #\vec{v}# langs de uitgestoken duim en #\vec{w}# langs de uitgestoken wijsvinger van de rechterhand ligt, dan wijst de vector #\vec{u}# in de richting van de uitgestoken middelvinger.
Het plaatje hieronder geeft een rechtshandig georiënteerde basis weer.
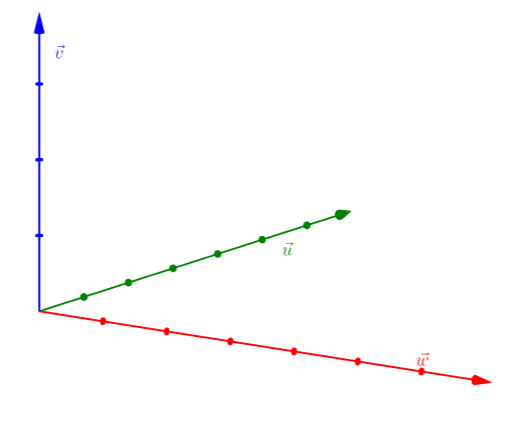
De manier om te bezien of een basis rechtshandig georiënteerd is, heet ook wel de kurkentrekkerregel.
Als een basis niet rechtshandig georiënteerd is, dan is maar één andere mogelijkheid: zij is linkshandig georiënteerd. Als #\vec{v}#, #\vec{w}#, #\vec{u}# rechtshandig georiënteerd is, dan is #\vec{w}#, #\vec{v}#, #\vec{u}# linkshandig georiënteerd.
Het uitproduct
Het uitproduct #\vec{v} \times \vec{w}# van de vectoren #\vec{v}# en #\vec{w}# is de vector \[\vec{v}\times\vec{w}=\parallel\vec{v}\parallel\cdot\parallel\vec{w}\parallel\cdot \sin(\varphi)\cdot\vec{u}\] waarbij
- #\varphi# de korte hoek is tussen #\vec{v}# en #\vec{w}# (zodat #0\leq \varphi \leq \pi#),
- #\vec{u}# de vector ter lengte #1# is die loodrecht staat op #\vec{v}# en #\vec{w}#, zodanig dat #\vec{v}#, #\vec{w}#, #\vec{u}# rechtshandig georiënteerd is als #\varphi\ne0,\pi#.
De vectoren #\vec{v}# en #\vec{w}# liggen dan en slechts dan op één lijn door de oorsprong als geldt #\varphi=0# of #\pi#. In beide gevallen geldt #\sin(\varphi) = 0#, zodat #\vec{v}\times\vec{w}=\vec{0}#. De oriëntatie van de vectoren #\vec{v}#, #\vec{w}# en #\vec{u}# is in dit geval niet gedefinieerd.
We kiezen hier voor de korte hoek tussen de vectoren #\vec{v}# en #\vec{w}#. De georiënteerde hoek tussen #\vec{v}# en #\vec{w}# is namelijk niet gedefinieerd: het vlak door de oorsprong, #\vec{v}# en #\vec{w}# heeft, zoals elk vlak in de ruimte, niet vanzelf een boven- en onderkant. In de 2-dimensionale theorie Inproduct en uitproduct bekijken we het platte vlak als het ware van boven. De georiënteerde hoek tussen de #x#-as en de #y#-as, of liever tussen #\rv{1,0}# en #\rv{0,1}#, wordt gemeten door tegen de klok in van de één naar de ander te draaien. Als we deze coördinaten zien als de eerste twee coördinaten van de ruimte, dan komt dit overeen met de rechtshandige basis #\rv{1,0,0}# (op de #x#-as), #\rv{0,1,0}# (op de #y#-as), en #\rv{0,0,1}# (op de #z#-as). Van boven kijken naar het platte vlak is dus te omschrijven als het kijken vanuit de positie van de derde basisvector van een rechtshandig georiënteerde basis. Met andere woorden, pas wanneer we een oriëntatie (zoals `tegen de klok in' of `van #\vec{v}# naar #\vec{w}# draaien') in het vlak vastleggen, kunnen we van een georiënteerde hoek tussen twee vectoren spreken. Een georiënteerde hoek is dus geen vanzelfsprekend begrip. Dit verklaart waarom we de georiënteerde hoek tussen #\vec{v}# en #\vec{w}# vermijden in de definitie van het uitproduct in de ruimte.
De scalar van de vector #\vec{u}# in de definitie van het uitproduct zal nooit negatief zijn, want #\sin(\varphi)\ge0# vanwege het feit dat #\varphi# de korte hoek tussen #\vec{v}# en #\vec{w}# beschrijft.
De lengte van #\vec{v}\times\vec{w}# is #\parallel\vec{v}\parallel\cdot\parallel\vec{w}\parallel\cdot\sin(\varphi)#. Hebben de vectoren #\vec{v}# en #\vec{w}# bijvoorbeeld allebei lengte #4# en is de hoek tussen de twee vectoren gelijk aan #60^{\circ}#, dan is
\[\vec{v}\times \vec{w} = 4\cdot 4\cdot \sin\left( 60^{\circ}\right) \cdot\vec{u}= 4\cdot 4\cdot \frac{1}{2}\sqrt{3}\cdot \vec{u}= 8\sqrt{3}\cdot\vec{u}\tiny,
\]waarbij #\vec{u}# de unieke vector van lengte #1# is, zodat #\vec{v}#, #\vec{w}#, #\vec{u}# rechtshandig georiënteerd is.
In de literatuur komen ook andere notaties van het uitproduct voor, zoals #\vec{v}\wedge\vec{w}#.
Het uitproduct wordt ook wel uitwendig product, vectorproduct, of kruisproduct genoemd.
Het uitproduct in 2 dimensies van de vectoren #\vec{v}# en #\vec{w}# voldoet aan #{\vec{v}\times\vec{w} } = {\parallel\vec{v}\parallel\cdot \parallel\vec{w}\parallel}\cdot \sin(\varphi) #. Als we het vlak als deel van de ruimte zien, dan is dit, op een teken na, de scalar van de vector #\vec{u}# loodrecht op dat vlak die voorkomt in bovenstaande definitie van het uitproduct in drie dimensies.
Het uitproduct in termen van twee lengtes
Laat #\vec{v}# en #\vec{w}# twee vectoren zijn die niet samen op een lijn door de oorsprong liggen. Geef met #\vec{u}# de vector van lengte #1# aan die loodrecht op #\vec{v}# en #\vec{w}# staat, zodanig dat #\vec{v}#, #\vec{w}# en #\vec{u}# rechtshandig georiënteerd is. Dan is het uitproduct #\vec{v}\times\vec{w}# gelijk aan #\lambda\cdot\vec{u}#, waarbij #\lambda# het product is van de lengte #\parallel\vec{v}\parallel# van #\vec{v}# en de afstand van het eindpunt van #\vec{w}# tot de lijn door #\vec{0}# met richtingsvector #\vec{v}#.
In het bijzonder is #\lambda# gelijk aan de dubbele oppervlakte van de driehoek met hoekpunten #\vec{0}#, #\vec{v}# en #\vec{w}#, ofwel aan de oppervlakte van het parallellogram opgespannen door #\vec{v}# en #\vec{w}# (dat wil zeggen: met hoekpunten #\vec{0}#, #\vec{v}#, #\vec{w}# en #\vec{v}+\vec{w}#).
Dit volgt direct uit de definitie van #\sin(\varphi)# toegepast op de driehoek #OAB#, waarbij #O# de oorsprong is, #A# het eindpunt van de representant van #\vec{w}# met beginpunt in de oorsprong, en #B# de loodrechte projectie van #A# op de lijn door #O# en het eindpunt van de representant van #\vec{v}# die in de oorsprong geplaatst is. Zie onderstaande figuur.
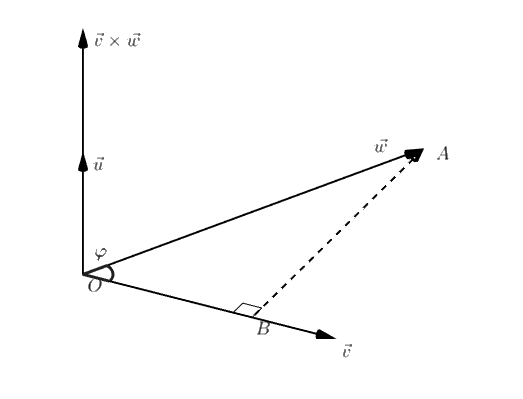
De laatste bewering volgt uit de lengte-maal-hoogte wet voor het oppervlak van een parallellogram, waarbij de lengte gelijk is aan #\parallel\vec{v}\parallel# en de hoogte gelijk is aan #\parallel\vec{w}\parallel \cdot \sin( \varphi )#.
De formule voor het uitproduct geeft
\[\vec{e}_{2}\times\vec{e}_{2}=\parallel\vec{e}_{2}\parallel\cdot\parallel\vec{e}_{2}\parallel\cdot \sin(\varphi)\cdot\vec{u}\] waarbij
- #\varphi# de (kortste) hoek is tussen #\vec{e}_{2}# en #\vec{e}_{2}#,
- #\vec{u}# de vector ter lengte #1# is die loodrecht staat op #\vec{e}_{2}# en #\vec{e}_{2}#, zodanig dat #\vec{e}_{2}#, #\vec{e}_{2}#, #\vec{u}# rechtshandig georiënteerd is.
De vier factoren van het rechter lid van de formule kunnen we als volgt bepalen:
- De lengtes #\parallel\vec{e}_{2}\parallel# en #\parallel\vec{e}_{2}\parallel# zijn beide gelijk aan #1# omdat de basis orthonormaal is.
- De sinus van de hoek #\varphi# is #0# omdat #\vec{e}_{2}# en #\vec{e}_{2}# gelijk zijn.
- De vector #\vec{u}# is # \vec{0} # omdat de vectoren #\vec{e}_2# en #\vec{e}_2# samen met #\vec{0}# op een lijn liggen.

omptest.org als je een OMPT examen moet maken.



