Vector calculus in plane and space: The Cross Product
 The concept of volume in space
The concept of volume in space
In the theory the concept of space in the plane we got to know area as a way to measure the size of geometric objects in the plane, such as triangles, rectangles, and circles. Its one-dimensional counterpart is length. Similarly, we can measure the size of geometric objects in space using the concept of volume. The volume shows how much space the geometric object takes.
We will use the term surface in space. Imagine a patchwork quilt (in space) whose patches are neatly fitting (2-dimensional, not necessarily planar) regions, wherein each patch has a suitable flat surface of the space, so that the perpendicular projection of the patch is a bijective image (i.e., never transmits more than one point to a given point of the flat surface) whose image is an region in the plane. The surface has no edge: each point on the edge of a piece of the quilt is also on another patch.
A body in the space is a subset of the space comprising all the points that lie within a certain surface. This surface is referred to as the edge of the body; the surface itself cannot have an edge and should comprise one piece.
The edge of a sphere is a spherical edge. A body that fits into a sphere, is referred to as limited.
The surface of the edge of the body is referred to as the area of the region.
An example of a surface in the space that has no edge, is a spherical surface that we call a sphere. Two surfaces that are faraway from each other form a surface that does not comprise one piece.
The edge of a limited body is not necessarily a spherical surface: imagine a tire (without a valve) or a pretzel. That kind of surface is called a torus. The corresponding body is, as it were (apart from deformation), a sphere with a hole beaten through. There are other examples: such as the globe with multiple holes.
The eight quadrants in the coordinate space are not limited, they are unlimited.
We are particularly interested in bodies whose 'patches' are parallelograms. Below we will enter the main examples.
Take three vectors #\vec{u}#, #\vec{v}#, #\vec{w}# that form a basis of the space. The body of the eight vertices #\vec{0}#, #\vec{u}#, #\vec{v}#, #\vec{w}#, #\vec{u}+\vec{v}#, #\vec{v}+\vec{w}#, #\vec{u}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}# is called a parallelepiped. The parallelepiped is outlined in the figure below.
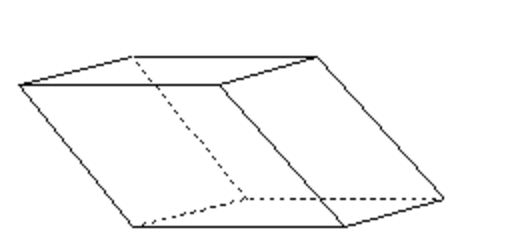
If the three vectors #\vec{u}#, #\vec{v}#, #\vec{w}# are mutually perpendicular, the parallelepiped is also known as a beam. If, additionally, the three vectors have the same length, the body is also known as a cube.
The edge of the parallelepiped is a surface with the following 'patches', which are often referred to as side faces, and parallelograms. They are defined by their vertices:
- #\vec{0}#, #\vec{u}#, #\vec{v}#, #\vec{u}+\vec{v}#
- #\vec{0}#, #\vec{v}#, #\vec{w}#, #\vec{v}+\vec{w}#
- #\vec{0}#, #\vec{u}#, #\vec{w}#, #\vec{u}+\vec{w}#
- #\vec{w}#, #\vec{u}+\vec{w}#, #\vec{v}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}#
- #\vec{u}#, #\vec{u}+\vec{v}#, #\vec{u}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}#
- #\vec{v}#, #\vec{u}+\vec{v}#, #\vec{v}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}#
We capture the volume of a number of special bodies with the following characteristics.
- The volume of a beam with sides of lengths #a#, #b#, and #c# is #a\cdot b\cdot c#.
- If #A# is a body is that can be obtained from #B# by displacement, rotation, and mirroring in the plane, #A# and #B# have the same volume.
- If two bodies only overlap on the edges, the volume of their union is equal to the sum of the volume of the two bodies.
- If a body #A# is set in a body #B#, the volume of #A# is less than, or equal to, the volume of #B#.
- If #U# is a surface in a flat plane #V# through #\vec{0}#, #\vec{v}# is a vector, and #L# is the body comprising all points of the form #\vec{u}+\lambda\cdot\vec{v}#, wherein #\vec{u}# belongs to #U# and #\lambda\in\ivcc{0}{1}#, then the volume of #L# is equal to #h\cdot {\rm Opp}(U)#, wherein #h# is the distance from #\vec{v}# to #V# and #{\rm Opp}(U)# is the surface of #U#.
Length, area, and volume can be measured in physical quantities, respectively as #\rm m#, #{\rm m}^2# and #{\rm m}^3# , but this is often omitted. Instead of volume one also speaks contents.
In the case of #a=b=c=1# the first rule gives the starting point for volume: if length, height, and width are the unit of length, for example, #1 {\rm\; m}#, the volume of the cube with sides of length #1# is the unit of volume, in the example #1 {\rm\; m}^3#. If #a#, #b#, #c# are natural numbers, then #a\cdot b\cdot c# unit cubes fit exactly in the beam, and the third rule gives that the volume is #a\cdot b\cdot c#.
The second rule makes it possible to determine that the volume of a parallelepiped is equal to the area of a face (a maximum 'patch' of the edge that fits in a flat surface) times the height of the opposite face. The fifth rule is a more general version of that.
The fourth rule allows us to estimate the volume of a body #L#:
- if #L# fits in a set of beams that only intersect at the edges, then the sum of the volume of those beams is the lower limit of the volume of #L#;
- if #L# fits entirely within the set of a group of bars, then the sum of the volumes of these beams is the upper limit of the volume of #L#.
This is how we can approach the real number that is the volume of #L#. Using limits, similar to those in Riemann exercises about integration, can we even define the volume of #L#.
Rule 5 can be understood with the aid of a parallelepiped, as is shown below:
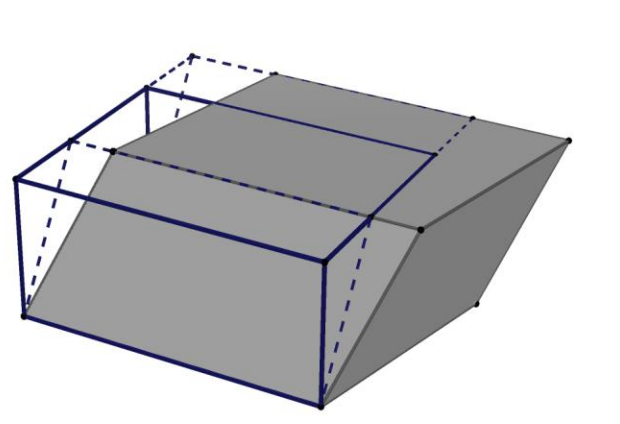
The volume of the beam is known. First, look at the differences between the beam and the parallelepiped, whose contours are dotted lines. The portion of the beam which is not included in the parallelepiped can be transferred into the portion of the parallelepiped that is not in the beam. Thanks to rule 2, the parallelepiped and the beam have the same volume. This same reasoning shows that the parallelepiped with the dotted outline and the gray parallelepiped have the same volume.
There is a more general version of rule 5 which uses the specific integration. If the points of the body #L# have all #z#-coordinates in the closed interval #\ivcc{a}{b}#, then the content of #L# is equal to #\int_a^b A(z)\,\dd z#, wherein #A(z)# is the area of the cross-section of #L# with the horizontal plane at a height #z#.

Or visit omptest.org if jou are taking an OMPT exam.



