Vectorrekening in vlak en ruimte: Het uitproduct
 Het begrip inhoud in de ruimte
Het begrip inhoud in de ruimte
In de theorie Het begrip oppervlakte in het vlak hebben we oppervlakte leren kennen als een manier om de grootte van meetkundige objecten in het platte vlak, als driehoeken, rechthoeken en cirkels, te meten. De één-dimensionale tegenhanger is lengte. Op vergelijkbare manier meten we de grootte van meetkundige objecten in de ruimte met behulp van het begrip inhoud. De inhoud geeft aan hoeveel ruimte het meetkundige object inneemt.
We gebruiken hierbij het begrip oppervlak in de ruimte. Denk hierbij aan een lappendeken (in de ruimte) waarvan de lappen netjes aansluitende (2-dimensionale, niet noodzakelijk platte) gebieden zijn, waarbij er voor elke lap een geschikt plat vlak van de ruimte bestaat zodat de loodrechte projectie van de lap erop een bijectieve afbeelding is (dus nooit meer dan één punt naar een gegeven punt van het platte vlak zendt) met als beeld een gebied in het vlak. Het oppervlak heeft geen rand: elk punt op de rand van een lap uit de lappendeken ligt ook op een andere lap.
Een lichaam in de ruimte is een deelverzameling van de ruimte bestaande uit alle punten die binnen een bepaald oppervlak liggen. Dat oppervlak wordt de rand van het lichaam genoemd; het oppervlak mag zelf geen rand hebben en moet uit één stuk bestaan.
Een bol heeft als rand een boloppervlak. Een lichaam dat in een bol past, heet begrensd.
De oppervlakte van de rand van het lichaam wordt de oppervlakte van het gebied genoemd.
Een voorbeeld van een oppervlak in de ruimte dat geen rand heeft, is een boloppervlak; het wordt ook wel een sfeer genoemd. Twee ver van elkaar liggende oppervlakken vormen tezamen een oppervlak dat niet uit één stuk bestaat.
De rand van een begrensd lichaam hoeft geen boloppervlak te zijn: denk aan de fietsband (zonder ventiel) of de krakeling. Zo'n oppervlak heet een torus. Het bijbehorende lichaam is als het ware (op vervorming na) een bol waar een gat doorheen geslagen is. Er zijn ook andere voorbeelden: de bol waar meer gaten doorheen geslagen zijn.
De acht kwadranten in de coördinaatruimte zijn niet begrensd, oftewel onbegrensd.
We zijn vooral geïnteresseerd in lichamen waarvan de `lappen' parallellogrammen zijn. Hieronder voeren we de belangrijkste voorbeelden in.
Neem drie vectoren #\vec{u}#, #\vec{v}#, #\vec{w}# die een basis van de ruimte vormen. Het lichaam met de acht hoekpunten #\vec{0}#, #\vec{u}#, #\vec{v}#, #\vec{w}#, #\vec{u}+\vec{v}#, #\vec{v}+\vec{w}#, #\vec{u}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}# heet een parallellepipedum. In de figuur hieronder is een parallellepipedum geschetst.
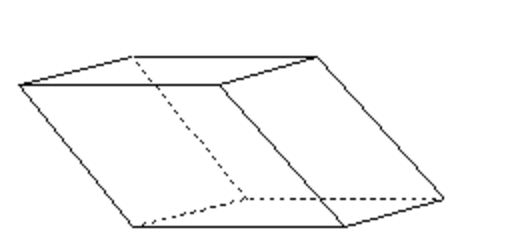
Als de drie vectoren #\vec{u}#, #\vec{v}#, #\vec{w}# onderling loodrecht zijn, dan wordt het parallellepipedum ook wel een balk genoemd. Als de drie vectoren bovendien dezelfde lengte hebben dan heet het lichaam ook wel een kubus.
De rand van het parallellepipedum is een oppervlak met de volgende `lappen' die vaak zijvlakken genoemd worden en parallellogrammen. Ze worden bepaald door hun hoekpunten:
- #\vec{0}#, #\vec{u}#, #\vec{v}#, #\vec{u}+\vec{v}#
- #\vec{0}#, #\vec{v}#, #\vec{w}#, #\vec{v}+\vec{w}#
- #\vec{0}#, #\vec{u}#, #\vec{w}#, #\vec{u}+\vec{w}#
- #\vec{w}#, #\vec{u}+\vec{w}#, #\vec{v}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}#
- #\vec{u}#, #\vec{u}+\vec{v}#, #\vec{u}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}#
- #\vec{v}#, #\vec{u}+\vec{v}#, #\vec{v}+\vec{w}#, #\vec{u}+\vec{v}+\vec{w}#
We leggen de inhoud van een aantal speciale lichamen vast met behulp van de volgende basiseigenschappen.
- De inhoud van een balk met zijden ter lengte #a#, #b# en #c# is #a\cdot b\cdot c#.
- Als #A# een lichaam is dat uit #B# verkregen kan worden door verschuiving, draaiing en spiegeling in het vlak, dan hebben #A# en #B# dezelfde inhoud.
- Als twee lichamen elkaar alleen op de randen overlappen, dan is de inhoud van hun vereniging gelijk aan de som van de inhouden van de twee lichamen.
- Als een lichaam #A# in een lichaam #B# ligt, dan is de inhoud van #A# kleiner dan of gelijk aan de inhoud van #B#.
- Als #U# een oppervlak in een plat vlak #V# door #\vec{0}# is, #\vec{v}# een vector, en #L# het lichaam bestaande uit alle punten van de vorm #\vec{u}+\lambda\cdot\vec{v}#, waarbij #\vec{u}# tot #U# behoort en #\lambda\in\ivcc{0}{1}#, dan is de inhoud van #L# gelijk aan #h\cdot {\rm Opp}(U)#, waarbij #h# de afstand van #\vec{v}# tot #V# is en #{\rm Opp}(U)# de oppervlakte van #U#.
Lengte, oppervlakte en inhoud kunnen worden gemeten in fysieke grootheden als respectievelijk #\rm m#, #{\rm m}^2# en #{\rm m}^3#, maar dat laten we vaak achterwege. In plaats van inhoud spreekt men ook wel van volume.
De eerste regel geeft in het geval #a=b=c=1# het uitgangspunt voor inhoud: als lengte, hoogte en breedte de eenheid van lengte, bijvoorbeeld #1 {\rm\; m}#, zijn, dan is de inhoud van de kubus met zijden ter lengte #1# de eenheid van inhoud, in het voorbeeld #1 {\rm\; m}^3#. Als #a#, #b#, #c# natuurlijke getallen zijn, dan passen er precies #a\cdot b\cdot c# eenheidskubussen in de balk, en geeft de derde regel dat de inhoud #a\cdot b\cdot c# is.
De tweede regel maakt het mogelijk om te beredeneren dat de inhoud van een parallellepipedum gelijk is aan de oppervlakte van een zijvlak (een maximale `lap' van de rand die in een plat vlak past) maal de hoogte van het overstaande zijvlak. De vijfde regel is een algemenere versie hiervan.
Met behulp van de vierde regel kunnen we de inhoud van een lichaam #L# schatten:
- als een vereniging van balken die elkaar alleen in de randen snijden, in #L# past, dan is de som van de inhouden van die balken een ondergrens van de inhoud van #L#;
- als #L# volledig binnen de vereniging van een stel balken past, dan is de som van de inhouden van die balken een bovengrens van de inhoud van #L#.
Zo kunnen we het reële getal benaderen dat de inhoud van #L# is. Met behulp van limieten, vergelijkbaar met de Riemannsommen bij integratie, kunnen we zo zelfs de inhoud van #L# exact definiëren.
Regel 5 is te begrijpen aan de hand van een parallellepipedum, zoals hieronder getekend:
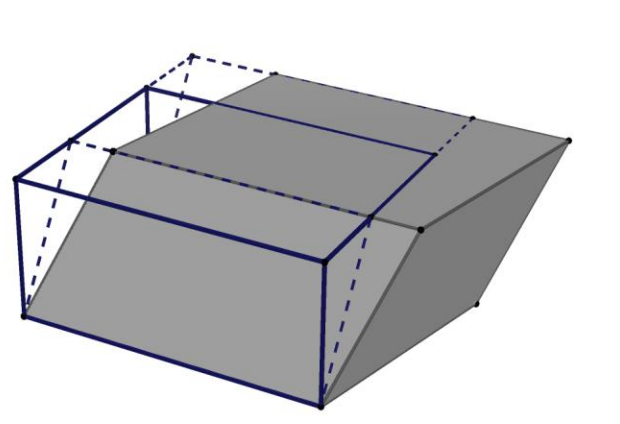
De inhoud van de balk is bekend. Bekijk eerst de verschillen van de balk met het parallellepipedum waarvan de contouren gestippeld zijn. Het stuk van de balk dat niet in het parallellepipedum zit is over te voeren in het stuk van het parallellepipedum dat niet in de balk zit. Dankzij regel 2 hebben balk en parallellepipedum dezelfde inhoud. Eenzelfde redenering laat zien dat het parallellepipedum met de gestippelde contouren en het grijze parallellepipedum dezelfde inhoud hebben.
Er is een algemenere versie van regel 5 die de bepaalde integratie gebruikt. Als de punten van het lichaam #L# alle #z#-coördinaten in het gesloten interval #\ivcc{a}{b}# hebben, dan is de inhoud van #L# gelijk aan #\int_a^b A(z)\,\dd z#, waarbij #A(z)# de oppervlakte van de doorsnee van #L# met het horizontale vlak op hoogte #z# is.
Het parallellepipedum is immers een kubus met zijden ter lengte \[\parallel \vec{e}_1\parallel=\parallel \vec{e}_2\parallel=\parallel \vec{e}_3\parallel=1\tiny.\]

omptest.org als je een OMPT examen moet maken.



