Vector calculus in plane and space: Vectors in Planes and Space
 The notion of vector
The notion of vector
In the plane and space we often work with vectors.
Vector
By vector we mean an arrow in the plane or space with a certain direction and length. In other words: a vector is a line segment which has a direction; the position of the vector in the plane or the space is not important. The norm or simply length of the vector is the length of the line segment.
When we drag a vector, so that its starting point is located elsewhere (but the direction and length remain unchanged), we consider this new arrow as a representative of the same vector.
Vectors are usually denoted by a character with a horizontal arrow above, which points to the right:\[\vec{v}\] The vector with a representative has a starting point #P# and an end point #Q# also indicated by #\vec{PQ}#.
There is one special vector, the vector of length \(0\). This vector does not provide a direction. We call this vector the null vector or zero vector and refer to it by \(\vec{0}\).
We now indicate how we can determine a vector by means of a point of the plane or space.
Correspondence between vector and point
In future, we will often encounter a chosen origin #O# in the plane or in the space. In situations such as this, we usually let the vector start at the origin. The vector is then solely determined by the endpoint, meaning that vectors can be seen as points of the space. The point #P# is then identified with the vector #\vec{OP}#. We then say that the vector #\vec{OP}# corresponds to the point #P#.
We next indicate how the length of a vector in #\mathbb{R}^2# or #\mathbb{R}^3# can be expressed in terms of coordinates.
The length of a vector in coordinates
The length of a vector can be expressed in coordinates as follows.
- The length of the vector #\rv{x,y}# in the plane #{\mathbb R}^2# is #\sqrt{x^2+y^2}#.
- The length of the vector #\rv{x,y,z}# in the space #{\mathbb R}^3# is #\sqrt{x^2+y^2+z^2}#.
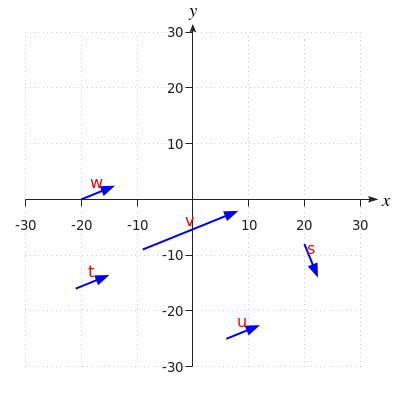
#s# does not have the right direction.
#v# does not have the right length.
If you drag the starting point from #t#, #u#, or #w# to #\rv{0,0}#, then the end point shows up at #\rv{5.6,2.2}#.

Or visit omptest.org if jou are taking an OMPT exam.