Vector calculus in plane and space: Distances, Angles and Inner Product
 Properties of the dot product
Properties of the dot product
The following properties make calculating the dot product easy and play a role in the explicit formulas that we will derive later on as we calculate using coordinates.
Properties of the dot product
Let #\vec{u}#, #\vec{v}#, and #\vec{w}# be vectors, and #\lambda# and #\mu# be scalars.
- The dot product of a vector with itself is the square of the length, or #\parallel\vec{u}\parallel = \sqrt{\vec{u}\cdot \vec{u}}#.
- The dot product #\vec{u}\cdot \vec{u}# is not negative for each vector #\vec{u}#, and is only equal to #0# if #\vec{u}=\vec{0}#.
- Symmetry: #\vec{u}\cdot \vec{v} = \vec{v}\cdot \vec{u}# .
- Mixed associativity with respect to scalar multiplication: \[\lambda \cdot\left(\vec{u}\cdot\vec{v}\right) = \left(\lambda \cdot\vec{u}\right)\cdot \vec{v} = \vec{u}\cdot
\left(\lambda \cdot\vec{v}\right)\tiny.\] - Additivity in each argument:
\[
\begin{array}{lcr}\vec{u}\cdot(\vec{v}+\vec{w}) &=& (\vec{u}\cdot \vec{v}) + (\vec{u}\cdot \vec{w}),\\ (\vec{v} + \vec{w})\cdot \vec{u} &=& (\vec{v} \cdot \vec{u}) + (\vec{w}\cdot\vec{u})\end{array}
\] - The dot product #\vec{u}\cdot\vec{v}# is exactly then the same as #0# if #\vec{u}# and #\vec{v}# are perpendicular to each other (another way of saying: orthogonal).
1. If we take #\vec{u}# for #\vec{v}#, the shared angle is #0^\circ#, which results in the fact that the cosine equals #1#, so #\vec{u}\cdot \vec{u} = \parallel\vec{u}\parallel^2# . So \[\parallel\vec{u}\parallel = \sqrt{\vec{u}\cdot \vec{u}}\tiny.\] Note that in any case the dot product is equal to #0# if one of the two vectors is the zero vector. The zero vector is orthogonal to each vector (the zero vector does not have a direction, but this is a convenient agreement).
2. The dot product #\vec{u}\cdot \vec{u}# is the square of the length of the vector #\vec{u}# because of 1, and thus not negative. If the dot product is equal to #0# , then #\vec{u}# is a vector of length #0#, and therefore must be the zero vector.
3. The angle between #\vec{v}# and #\vec{u}# is #-\varphi#, so the following applies \[\vec{v}\cdot\vec{u} = \parallel \vec{v}\parallel\cdot\parallel\vec{u}\parallel\cdot\cos(-\varphi) = \parallel \vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\cos(\varphi) = \vec{u}\cdot\vec{v}\tiny.\]
4. If #\lambda=0# all elements equal #0# and we are done with the proof. Assume, therefore, that #\lambda# is not equal to #0#. The angle between #\vec{u}# and #\lambda\cdot\vec{v}# is equal to #\varphi# if #\lambda\gt0#, and equal to #180^\circ-\varphi# if #\lambda\lt0#. Consequently, \[\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) = \parallel\vec{u}\parallel\cdot\parallel\lambda\cdot\vec{v}\parallel\cdot\cos(\varphi)=\lambda\cdot\left(\vec{u}\cdot\vec{v}\right)\] as #\lambda\gt0# and \[\begin{array}{rcl}\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) &=& \parallel\vec{u}\parallel\cdot\parallel\lambda\cdot\vec{v}\parallel\cdot\cos(180^\circ-\varphi)\\ &=&\left|\lambda\right|\cdot\parallel\vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\left(-\cos(\varphi)\right)\\ &=&\lambda\cdot\parallel\vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\cos(\varphi)\\ &=&\lambda\cdot\left(\vec{u}\cdot\vec{v}\right)\end{array}\] as #\lambda\lt0#.
We conclude that, in all cases #\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) = \lambda\cdot\left(\vec{u}\cdot\vec{v}\right)# applies. The other equality can be proven in the same way.
5. We start with the first of the first two equations: #\vec{u}\cdot(\vec{v}+\vec{w}) = (\vec{u}\cdot \vec{v}) + (\vec{u}\cdot \vec{w})#. If #\vec{u}=\vec{0}#, the equality is true, because all terms are equal #0#. Therefore, we may assume that this is not true, so #\parallel\vec{u}\parallel\ne0# and there is a unique line through the origin and #\vec{u}#. Call that line #\ell#.
It is sufficient to prove the equality in the case that #\parallel\vec{u}\parallel=1#. The general case then follows from the previous rule with #\lambda=\parallel\vec{u}\parallel# : \[\begin{array}{rcl}\vec{u}\cdot(\vec{v} + \vec{w}) &=&\lambda\cdot \left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot(\vec{v} + \vec{w})\right)\\&=&\lambda\cdot\left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{v} +\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{w}\right)\\&=&\lambda\cdot\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{v} +\lambda\cdot\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{w}\\&=&\left( \vec{u}\cdot\vec{v}\right) +\left(\vec{u}\cdot\vec{w}\right)\\\end{array}\] Note that #\parallel\frac{1}{\lambda}\cdot \vec{u}\parallel = \frac{1}{\lambda}\cdot\parallel\vec{u}\parallel=\frac{1}{\lambda}\cdot\lambda = 1#, so that in the case above, only the specific case with a vector of a length #1# was used.
It is sufficient to prove the first equality as #\parallel\vec{u}\parallel=1#. In this case, because of The dot product, in terms of lengths, #(\vec{u}\cdot\vec{y})\cdot \vec{u}# is the projection of #\vec{y}# on #\ell# for each vector #\vec{y}#. Let #A# be the endpoint of #\vec{v}#, #B# be the endpoint of #\vec{w}#, and #C# be the endpoint of #\vec{v}+\vec{w}#, all three placed at the origin. Give the projection of respectively #A#, #B#, and #C# on #\ell# with #P_A#, #P_B#, and #P_C#. In that case #(\vec{u}\cdot\vec{v})\cdot \vec{u}=\vec{OP_A}# , #(\vec{u}\cdot\vec{w})\cdot \vec{u}=\vec{OP_B}# and #\left(\vec{u}\cdot(\vec{v}+\vec{w})\right)\cdot \vec{u}=\vec{OP_C}#. The equality that we want to prove follows if we can demonstrate that #\vec{OP_A}+\vec{OP_B}=\vec{OP_C}#. See the figure below.
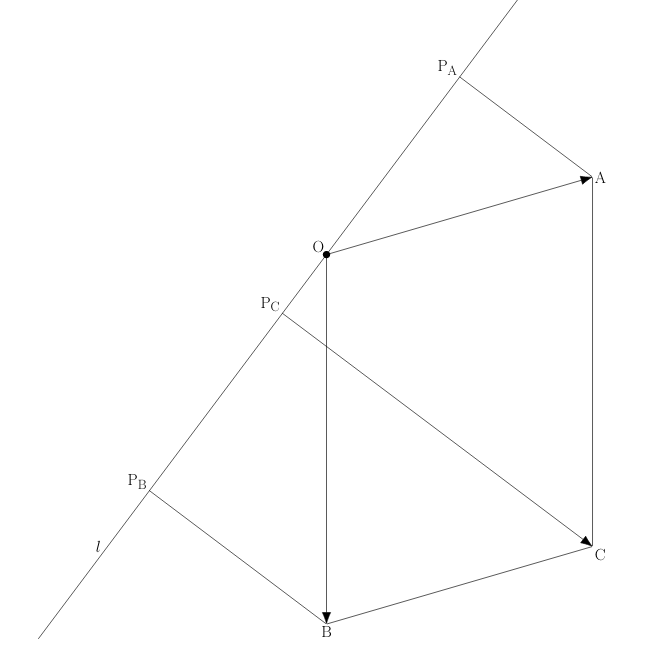
We will once more apply The dot product in terms of lengths, but now to the vector #\vec{v}# and the line #\ell#, which comprises all the scalar multiples of #\vec{u}#. In that case #\vec{P_BP_C}# is the projection of the vector #\vec{v}#, placed in #B#, onto #\ell#, so that # \vec{P_BP_C}=\vec{OP_A}#. Adding #\vec{OP_B}# on both sides gives #\vec{OP_C}=\vec{OP_A}+\vec{OP_B}#, which proves the requested equality.
The second equality follows from the first when applying the third rule: \[\begin{array}{rcl}(\vec{v}+\vec{w})\cdot\vec{u} &=&\vec{u}\cdot(\vec{v}+\vec{w})\\ &&\phantom{xxx}\color{blue}{\text{symmetry}}\\&=&(\vec{u}\cdot \vec{v})+(\vec{u}\cdot \vec{w})\\ &&\phantom{xxx}\color{blue}{\text{the first equality}}\\&=&(\vec{v}\cdot\vec{u})+(\vec{w}\cdot\vec{u})\\ &&\phantom{xxx}\color{blue}{\text{symmetry}}\end{array}\]
6. If #\vec{u}\cdot\vec{v}=0#, then #\parallel \vec{u}\parallel \cdot\parallel \vec{v}\parallel \cdot\cos(\varphi)=0# applies, which means there are three cases to identify:
- #\parallel \vec{u}\parallel =0#: which means that #\vec{u}=0#, in which case #\vec{u}# is, by definition, perpendicular to #\vec{v}#;
- #\parallel \vec{v}\parallel =0#: which means that #\vec{v}=0#, in which case #\vec{v}# is, by definition, perpendicular to #\vec{u}#;
- #\cos(\varphi)=0#: which means that #\varphi=\pm\frac{\pi}{2}#, that is to say: #\vec{u}# is perpendicular to #\vec{v}#.
The other implication (if #\vec{u}# and #\vec{v}# are mutually perpendicular, then #\vec{u}\cdot\vec{v}=0# applies) can be proven by reversing the arguments above.
Using the calculation rule mixed associativity with respect to scalar multiplication, we find
\[\begin{array}{rcl}\left(4\cdot \vec{u}\right)\cdot\left( 2\cdot\vec{v}\right)&=&4\cdot \left(\vec{u}\cdot\left( 2\cdot\vec{v}\right)\right)\\ &=&
8\cdot\left(\vec{u}\cdot \vec{v}\right)\\
&=&8\cdot 7\\
&=&56\\
\end{array}\]

Or visit omptest.org if jou are taking an OMPT exam.



