Basic algebra skills: Quadratic functions
The quadratic formula
We have seen how to quickly solve a quadratic equation using factorisation. However, not every equation can be solved with factorisation (at least, without taking roots). That is why, in this section, we will look at a general solution method that always works: the quadratic formula.
Completing the square
A quadratic polynomial in #x# can be written in such a way that the variable #x# only appears once:
\[ax^2+bx+c = a\cdot\left(\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4a\cdot c}{(2a)^2}\right)\tiny.\] This rewrite is called completing the square.
This can be seen by removing the brackets from the right-hand side.
Some examples:
\[\begin{array}{rcl}x^2+x+1&=&\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\\ x^2+2x+1&=&\left(x+1\right)^2\\ 2x^2+x+1&=&2\cdot\left(\left(x+\dfrac{1}{4}\right)^2+\dfrac{7}{16}\right)\\ x^2+x+2&=&\left(x+\dfrac{1}{2}\right)^2+\dfrac{7}{4}\\ x^2+3x+2&=& \left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4} \end{array}\]
We use this to solve quadratic equations.
Discriminant and ABC formula
Let #a#, #b#, #c# be real numbers with #a\ne0#. The equation #ax^2+bx+c=0# can be reduced to
\[x=\dfrac{-b - \sqrt{b^2-4a\cdot c}}{2a}\lor x=\dfrac{-b+ \sqrt{b^2-4a\cdot c}}{2a}\]
We call the expression #b^2-4a\cdot c# the discriminant of #a\cdot x^2+b\cdot x+c#. We often refer to it as #D#.
With this notation, we have \[x=\dfrac{-b - \sqrt{D}}{2a}\lor x=\dfrac{-b+ \sqrt{D}}{2a}\]
- If #D\lt 0#, then there are no solutions.
- If #D= 0#, then there is only one solution: #x=\dfrac{-b}{2a}#.
- If #D\gt 0#, then there are two solutions.
What we have described, is called the quadratic formula. Any quadratic equation can be solved with this formula.
We use the quadratic formula to determine the intersections of a parabola with the #x#-axis. What does this mean for the three cases we just saw? We now consider the case in which #a\gt0# (then, the graph is an upward opening parabola). If #a\lt0#, you get the same image as below by multiplying the left-hand side #ax^2+bx+c# by #-1# (in other words: by reflecting the graph over the #x#-axis).
If #D\gt0#, then the square root of a positive number is taken, and the equation #a\cdot x^2+b\cdot x+c=0# therefore has two different solutions. The parabola, that is, the graph of #a\cdot x^2+b\cdot x+c#, has #2# intersections with the #x#-axis.
If #D\lt0#, then there are no solutions, because taking the square root of a negative number does not yield a real number. The parabola then has no intersections with the #x#-axis.
If #D= 0#, then both solutions are the same, which means that there is only one unique solution: #x=\dfrac{-b}{2a}#. Here, the parabola is tangent to the #x#-axis.
We will now look at some examples where quadratic equations are solved using the quadratic formula and where the discriminant is used to determine how many solutions a quadratic equation has.
Use the quadratic formula:
\[x=\frac{-b-\sqrt{D}}{2a}\lor x=\frac{-b+\sqrt{D}}{2a}\]
with discriminant #D=b^2-4a\cdot c#.
\[\begin{array}{rcl}
a=2&b=5&c=3\\
&&\phantom{xx}\color{blue}{\text{a, b and c determined}}\\
(5)^2-4\cdot 2\cdot 3&=&400\\
&&\phantom{xx}\color{blue}{\text{discriminant calculated}}\\
x=\frac{-5-20}{4}&\lor&x=\frac{-5+20}{4}\\
&&\phantom{xx}\color{blue}{\text{quadratic formula used}}\\
x=-1&\lor&x=-{{3}\over{2}}\\
&&\phantom{xx}\color{blue}{\text{solution simplified}}\\
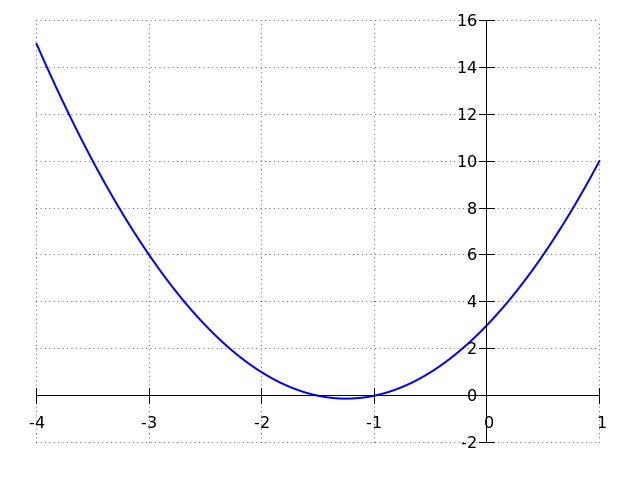
\end{array}\]The graph of the function #y=2 x^2+5 x+3# is drawn below. The #x#-coordinates of the meeting points of the graph and the #x#-axis are the solutions to the equation.
Or visit omptest.org if jou are taking an OMPT exam.
