Functions: Power functions and root functions
 Inverse functions
Inverse functions
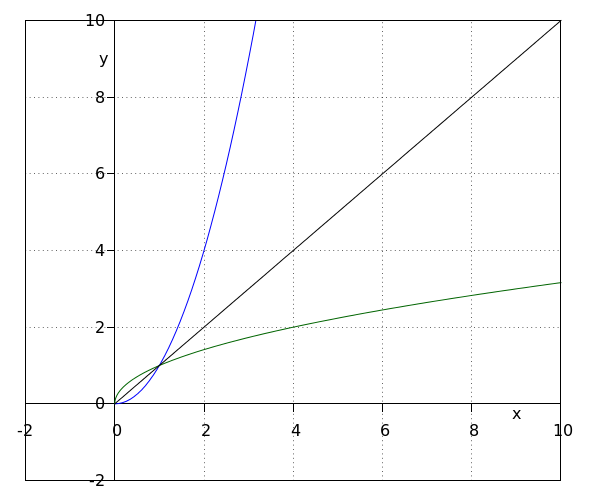
We take a look at the functions #\blue{f(x)}=\blue{x^2}# (solid) and #\green{g(x)}=\green{\sqrt{x}}# (dashed) on the domain #\ivco{0}{\infty}#.
For these functions we have #\blue f(\green{g(x)})=\left(\green{\sqrt{x}}\right)^\blue2=x# for all #x# in #\ivco{0}{\infty}#.
Therefore #\green{g(x)}# is called the inverse of #\blue{f(x)}#.
We also have #\green g(\blue{f(x)})=\green{\sqrt{\blue{x^2}}}=x# for all #x# in #\ivco{0}{\infty}#.
Therefore #\blue{f(x)}# is called the inverse of #\green{g(x)}#.
The function #\blue{f(x)}# has inverse function #\green{g(x)}# if \[\blue f(\green{g(x)})=x\]
From a geometrical perspective, the graph of the inverse of #\green{g(x)}# is the reflection of #\blue{f(x)}# over the line #y=x#.
We can also notate the inverse of #f(x)# by #f^{-1}(x)#.
When determining the inverse of a function, the domain of that function is important. The domain of #\blue{f(x)}# is the range of #\green{g(x)}# and the domain of #\green{g(x)}# is the range of #\blue{f(x)}#. Hence, the inverse function #\green{g(x)}# is defined on the range of function #\blue{f(x)}#.
Example
In the graph #\blue{f(x)}=\blue{(x+1)^2}# on the domain #x \ge -1# and its inverse #\green{g(x)}=\green{\sqrt{x}-1}# on the domain #x \ge 0#
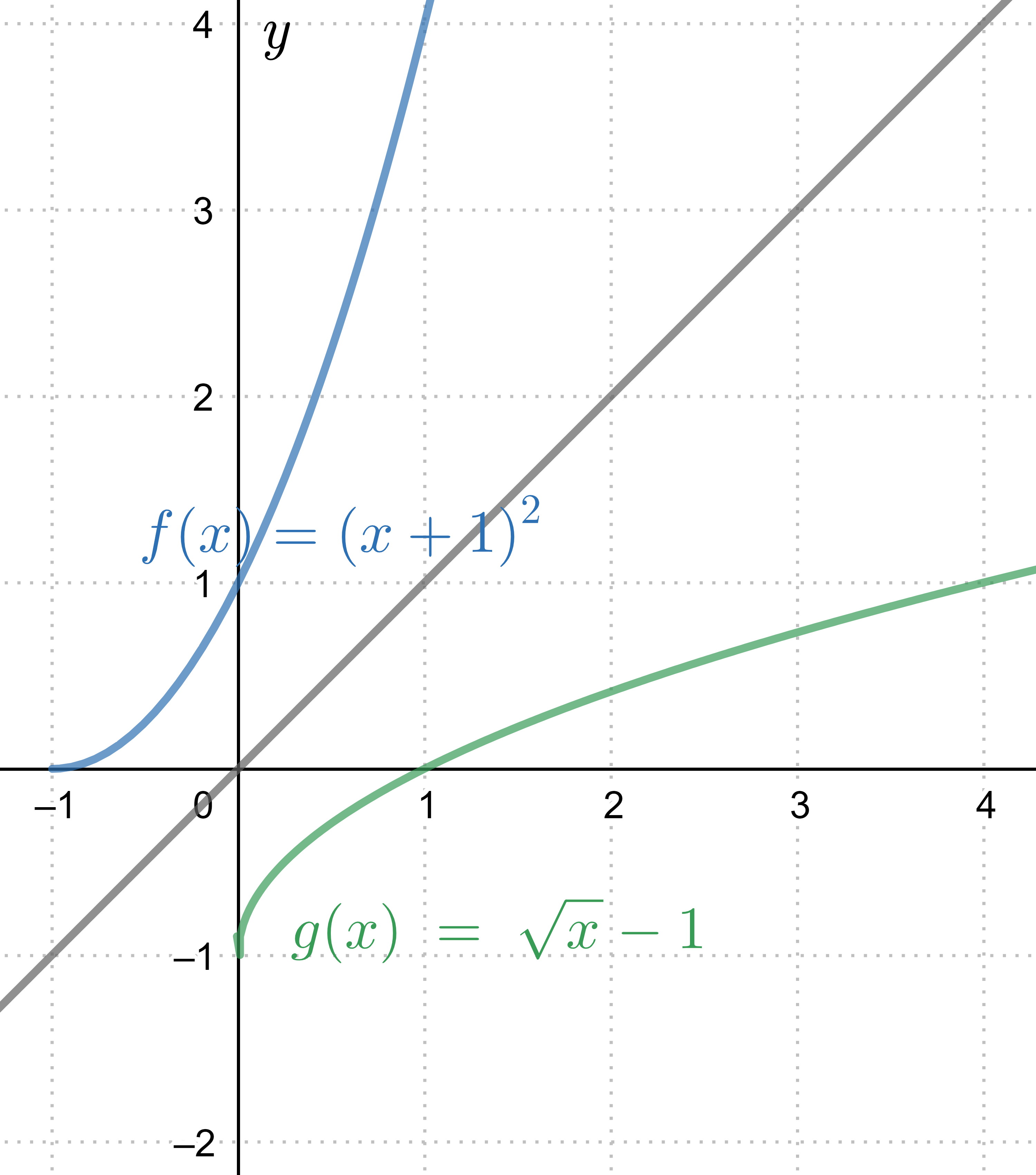
Determining inverse function
|
Procedure We determine the inverse function #\green{f^{-1}(x)}# of the function #\blue{f(x)}#. |
Example #\blue{f(x)}=\left(x-4\right)^2#. |
|
| Step 1 | Write the function as a formula, hence in the form #y=\ldots#. |
#y=\left(x-4\right)^2# |
| Step 2 | Isolate the variable #x# in the formula #y=\ldots#. This means that the formula is written as #x=\ldots#. |
#x=\sqrt{y}+4# |
| Step 3 | In the formula, change the #y# into #x# and #x# into #y#. |
#y=\sqrt{x}+4# |
| Step 4 | Replace #y# by #\green{f^{-1}(x)}#. |
#\green{f^{-1}(x)}=\sqrt{x}+4# |
#\begin{array}{rcl}
y&=&\sqrt{2\cdot x-3} \\ &&\phantom{xxx}\blue{\text{original function}}\\
y^2&=& 2\cdot x-3 \\ &&\phantom{xxx}\blue{\text{squared both sides}}\\
y^2+3&=&2\cdot x \\ &&\phantom{xxx}\blue{\text{both sides minus }-3}\\
{{y^2+3}\over{2}} &=&x \\ &&\phantom{xxx}\blue{\text{divided both by }2}\\
x&=&{{y^2+3}\over{2}} \\ &&\phantom{xxx}\blue{\text{swapped left and right }}\\
\end{array}#

Or visit omptest.org if jou are taking an OMPT exam.



