Higher degree inequalities

Functions: Higher degree polynomials

Higher degree inequalities

In the same manner as when solving a quadratic inequality, we can also solve an inequality with higher degree polynomials.

Solving a higher degree inequality

	Procedure	Example
	We solve the following inequality \[\blue{f(x)} \gt \green{g(x)}\] in which #\blue{f(x)}# and #\green{g(x)}# are polynomials.	#\blue{x^6+x^3+6}\ (solid)\gt \green{-2x^3+10}\ (dashed)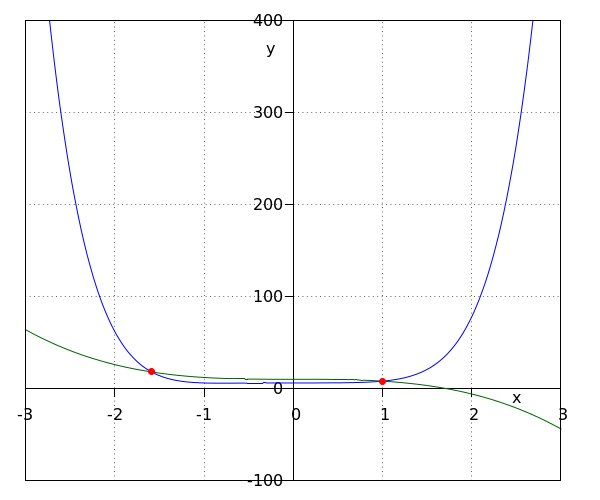# The solution is #x \lt \sqrt[3]{-4} \land x \gt 1#.
Step 1	We solve the equality \[\blue{f(x)} = \green{g(x)}\]
Step 2	We sketch the graphs #\blue{f(x)}# and #\green{g(x)}#.
Step 3	With the help of step 1 and 2, determine for which values of #x# the inequality holds. In a coordinate system, the biggest graph is the one above the other.

Please note that this procedure also holds for the inequality signs #\geq# and #\leq#, only now the #x#-values of the intersection points are also part of the solution.

All or noneIf no intersection points are found in step 1, then there are two options with regard to the solution of the inequality.

all points of #x# are a solution to the inequality. The inequality is always true.
no points of #x# are a solution to the inequality. The inequality is never true.

The same can happen as if in step 1 an intersection point is found, but when it's only a point of tangency. Then they are only equal in that point and the inequality is true or not.

Alternative step 2

Instead of sketching the graphs, we can also do step #2# by substituting a few #x#-values in #\blue{f(x)}# and #\green{g(x)}#, so we can see on which intervals the statement #\blue{f(x)}\gt \green{g(x)}# holds.

Only in the intersection points of #\blue{f(x)}# and #\green{g(x)}#, it can change which function is bigger. Therefore, taking one point in each interval is enough to know.

In the example above and on the right, the intersection points of #\blue{f(x)}# and #\green{g(x)}# are the #x# values #x = \sqrt[3]{-4}# and #x=1#. So, we choose a #x#-value smaller than # \sqrt[3]{-4}#, a #x#-value between #x= \sqrt[3]{-4}# and #x=1#, and a #x#-value larger than #1#. This gives us all information we need to know when #\blue{f(x)}# is larger than #\green{g(x)}#.

Example

In the example above, we substitute a few #x#-values.

#\blue f(-2)=62 \gt \green g(-2)=26 #

#\blue f(0)=6 \lt\green g(0)=10#

#\blue f(2)=78 \gt \green g(2)=-6#

Step 3 then gives us that the solution is #x \lt \sqrt[3]{-4} \land x \gt 1#, because the inequality holds for #x=-2# and #x=2#.

Solve #d# in the inequality
\[d^6-d^3+8\cdot d-28 \gt 8\cdot d-8\tiny\]
Give your answer in the form

#d \gt d_1\land d \lt d_2# or #d\lt d_1 \lor d \gt d_2#,
#d \lt d_1# or #d \gt d_1#,
#none# or #all#,

with the correct values of #d_1# and #d_2#.

#d\lt -4^{{{1}\over{3}}}\lor d\gt 5^{{{1}\over{3}}}#

Step 1	We solve the equality #d^6-d^3+8\cdot d-28=8\cdot d-8#. This is done like this: \[\begin{array}{rcl} d^6-d^3+8\cdot d-28&=&8\cdot d-8 \\ &&\phantom{xxx}\blue{\text{original equation}}\\ d^6-d^3-20&=&0 \\&&\phantom{xxx}\blue{\text{reduced to }0}\\ \left(d^3-5\right)\cdot \left(d^3+4\right)&=&0 \\&&\phantom{xxx}\blue{\text{left hand side factorized}}\\ d^3-5=0 &\lor& d^3+4=0 \\&&\phantom{xxx}\blue{A\cdot B=0 \text{ if and only if }A=0\lor B=0}\\ d=5^{{{1}\over{3}}} &\lor& d=-4^{{{1}\over{3}}} \\&&\phantom{xxx}\blue{\text{constant terms to the right hand side and taken the root}}\\ \end{array} \]
Step 2	We sketch the graphs #y=d^6-d^3+8\cdot d-28# (blue) and #y=8\cdot d-8# (green dashed).
Step 3	We can read the solutions to the inequality from the graph. \[d\lt -4^{{{1}\over{3}}}\lor d\gt 5^{{{1}\over{3}}}\]

New example