Rules for right-angled triangles

Trigonometry: Angles with sine, cosine and tangent

Rules for right-angled triangles

There is an important rule for right-angled triangles pertaining the ratio between the sides.

Pythagorean theorem

When it comes to the lengths of the sides of a right-angled triangle with a right angle #\orange C#, legs #\blue a# and #\green b# and hypotenuse (the longest side of a right-angled triangle) #\orange c#, the following rule applies:

\[\blue a^2+\green b^2=\orange c^2\]

We call this rule the Pythagorean theorem.

With this theorem, we can calculate the remaining side of a right-angled triangle of which we already know two sides.

For example, if we want to calculate the hypotenuse, we isolate #\orange c# in the Pythagorean theorem:

\[\orange c = \sqrt{\blue a ^2 + \green b^2}\]

In a right-angled triangle #ABC# with right angle #C# is #AB# the #\orange{\textbf{hypotenuse}}# and are #AC# and #BC# the legs of the triangle:

#AC# is the #\green{\textbf{adjacent leg}}# of #\blue \alpha#
#BC# is the #\blue{\textbf{opposite leg}}# of #\blue \alpha#

geogebra plaatje

In addition to the ratio between the sides of a right-angled triangle, there are important relationships between the sides and angles of a right-angled triangle.

Sine, cosine, and tangent in a right-angled triangle,

In a right-angled triangle #\triangle ABC# with right angle #C# we define:

#\sin(\alpha)=\frac{\text{opposite side}}{\text{hypotenuse}}=\frac{\blue a}{\orange c}#
#\cos(\alpha)=\frac{\text{adjacent side}}{\text{hypotenuse}}=\frac{\green b}{\orange c}#
#\tan(\alpha)=\frac{\text{opposite side}}{\text{adjacent side}}=\frac{\blue a}{\green b}#

We call #\sin# (sine), #\cos# (cosine) and #\tan# (tangent) trigonometric functions.

With these trigonometric functions we can calculate, using an angle and a side, the remaining sides in a right-angled triangle. We can also calculate the angle using two sides and the inverse.

Calculator

The buttons #\sin#, #\cos# and #\tan# are on your calculator. Note that your calculator is set to degrees instead of radians when working with degrees. We will later have a look at radians, but for now we'll only work with degrees.

The inverses of the trigonometric function #\sin^{-1}# or #\arcsin#, #\cos^{-1}# or #\arccos# and #\tan^{-1}# or #\arctan# are also on your calculator. We can use these to calculate the measure of an angle in a triangle of which we already know two sides.

Other angle

We have now given the expression for the angle #\blue \alpha#, but in the same way, we can also give expressions for angle #\green \beta#. In this case, the adjacent side is then equal to side #\blue a# and the opposite side adjacent to side #\green b#.

Given triangle #ABC# :

Calculate side #AC# exactly.

#AC=# #5#

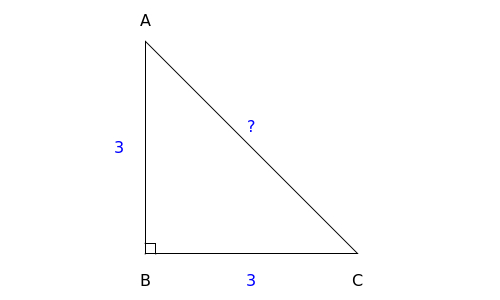
# \begin{array}{rcl}AB^2+BC^2&=&AC^2 \\ &&\phantom{xxx}\blue{\text{Pythagorean theorem}} \\
3^2+4^2&=&AC^2 \\ &&\phantom{xxx}\blue{AB=3 \text{ en } BC=4} \\
25&=&AC^2 \\ &&\phantom{xxx}\blue{\text{calculated}} \\
\sqrt{25}&=&AC \\ &&\phantom{xxx}\blue{\text{took root on both sides}} \\
AC&=&5 \\ &&\phantom{xxx}\blue{\text{swapped left and right, and simplified where possible}} \end {array} #

New example