Trigonometry: Trigonometric functions
 Transformations of trigonometric functions
Transformations of trigonometric functions
We have seen what the standard graphs of sine and cosine look like. We can also transform these functions.
We can transform the functions #f(x)=\sin(x)# and #g(x)=\cos(x)# in four ways. We will show these using the sine function, but the cosine works in the same way.
| Transformations | Examples | |
| 1 |
We shift the graph of #f(x)=\sin(x)# up by #\green q#. The new function becomes \[f(x)=\sin(x)+\green q\] The period and amplitude of the function remain the same, but the equilibrium becomes equal to #\green q#. |
Plaatje verticale translatie
|
| 2 |
We shift the graph of #f(x)=\sin(x)# to the right by #\blue p#. The new function becomes \[f(x)=\sin\left(x-\blue p\right)\] The period, amplitude and equilibrium remain the same. We call #\blue p# the phase shift. |
Plaatje horizontale translatie
|
| 3 |
We multiply the graph of #f(x)=\sin(x)# by #\purple a# relative to the #x#-axis. The new function becomes \[f(x)=\purple a \sin(x)\] The period and equilibrium remain the same, but the amplitude becomes equal to #\purple{\left| a \right|}#. When #\purple a \lt 0#, the graph reverses. This means it first falls instead of rises. If #\purple a =- 1#, the new function is a reflection of the old function across the #x#-axis. |
Plaatje vermenigvuldiging x-as
|
| 4 |
We multiply the graph of #f(x)=\sin(x)# by #\orange b# relative to the #y#-axis. This means we replace #x# with #\frac{1}{\orange b}x#. The new function becomes \[f(x)=\sin\left(\frac{1}{\orange b}x\right)\] The equilibrium and amplitude remain the same, but the period becomes equal to #\orange b \cdot 2 \pi#.
|
Plaatje vermenigvuldiging #y#-as.
|
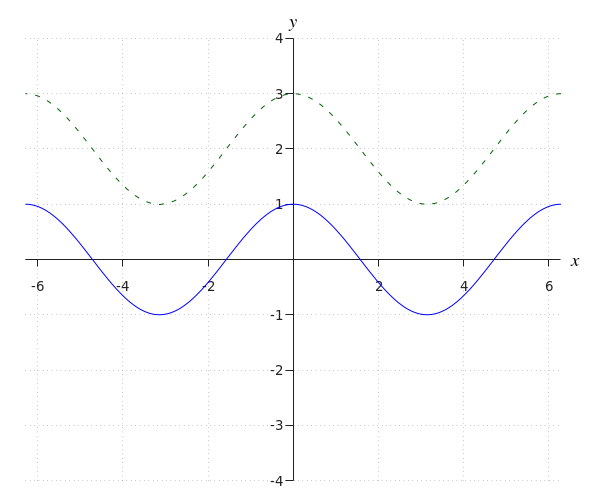
#y=# #\cos(x)+2#
In step 1 we saw that the green graph is obtained by shifting the blue graph upwards by #2#. Hence, we add #2# to the formula of the blue graph #y=\cos(x)#. This gives us the following formula for the green graph:
\[y=\cos(x)+2\]

Or visit omptest.org if jou are taking an OMPT exam.